【题目】如图,点A,C,D,E在Rt△MON的边上,∠MON=90°,AE⊥AB且AE=AB,BC⊥CD且BC=CD,BH⊥ON于点H,DF⊥ON于点F,OM=12,OE=6,BH=3,DF=4,FN=8,图中阴影部分的面积为________.

参考答案:
【答案】50
【解析】
易证△AEO≌△BAH,△BCH≌△CDF即可求得AO=BH,AH=EO,CH=DF,BH=CF,即可求得梯形DEOF的面积和△AEO,△ABH,△CGH,△CDF的面积,即可解题.
∵∠EAO+∠BAH=90°,∠EAO+∠AEO=90°,
∴∠BAH=∠AEO,
∵在△AEO和△BAH中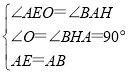 ,
,
∴△AEO≌△BAH(AAS),
同理△BCH≌△CDF(AAS),
∴AO=BG=3,AH=EO=6,CH=DF=4,BH=CF=3,
∵梯形DEOF的面积=![]() (EF+DH)FH=80,
(EF+DH)FH=80,
S△AEO=S△ABH=![]() AFAE=9,
AFAE=9,
S△BCH=S△CDF=![]() CHDH=6,
CHDH=6,
∴图中实线所围成的图形的面积S=80-2×9-2×6=50,
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图,直线a,b被直线c所截,a∥b,∠1=∠2.若∠3=40°,则∠4等于________
(2)如图,将三角形ABC沿BC方向平移3 cm得到三角形DEF,如果四边形ABFD周长是28 cm,则三角形ABC的周长是________cm.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校组织初二年级400名学生到威海参加拓展训练活动,已知用3辆小客车和1辆大客车每次可运送学生105人,用1辆小客车和2辆大客车每次可运送学生110人.
(1)每辆小客车和每辆大客车各能坐多少名学生?
(2)若计划租小客车m辆,大客车n辆,一次送完,且恰好每辆车都坐满:
①请你设计出所有的租车方案;
②若小客车每辆租金250元,大客车每辆租金350元,请选出最省线的租车方案,并求出最少租金.
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线l1平行于直线l2,直线l3、l4分别与l1、l2交于点B、F和A、E,点D是直线l3上一动点,DC∥AB交l4于点C.
(1)如图,当点D在l1、l2两线之间运动时,试找出∠BAD、∠DEF、∠ADE之间的关系,并说明理由;

(2)当点D在l1、l2两线外侧运动时,试探究∠BAD、∠DEF、∠ADE之间的关系(点D和B、F不重合),画出图形,给出结论,不必说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,都是由边长为1的正方体叠成的立体图形,例如第(1)个图形由1个正方体叠成,第(2)个图形由4个正方体叠成,第(3)个图形由10个正方体叠成,依次规律,第(8)个图形有多少个正方体叠成( )

A.120个B.121个C.122个D.123个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,一个点从数轴上的原点开始,先向右移动3个单位长度,再向左移动5个单位长度,可以看到终点表示的数是-2,已知点A,B是数轴上的点,请参照图并思考,完成下列各题.
(1)如果点A表示数-3,将点A向右移动7个单位长度,那么终点B表示的数是_____,A,B两点间的距离是_____;
(2)如果点A表示数3,将A点向左移动7个单位长度,再向右移动5个单位长度,那么终点表示的数是_____,A,B两点间的距离为_____;
(3)如果点A表示数-4,将A点向右移动168个单位长度,再向左移动256个单位长度,那么终点B表示的数是_____,A、B两点间的距离是_____;
(4)一般地,如果A点表示的数为m,将A点向右移动n个单位长度,再向左移动p个单位长度,那么请你猜想终点B表示什么数?A,B两点间的距离为多少?

-
科目: 来源: 题型:
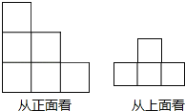
查看答案和解析>>【题目】用小立方块搭成的几何体.从正面看和从上面看的形状如图所示,问组成这样的几何体最多需要多少个立方块,最少需要多少个立方块?请画出最少和最多时从左面看到的形状.
相关试题

