【题目】某校组织初二年级400名学生到威海参加拓展训练活动,已知用3辆小客车和1辆大客车每次可运送学生105人,用1辆小客车和2辆大客车每次可运送学生110人.
(1)每辆小客车和每辆大客车各能坐多少名学生?
(2)若计划租小客车m辆,大客车n辆,一次送完,且恰好每辆车都坐满:
①请你设计出所有的租车方案;
②若小客车每辆租金250元,大客车每辆租金350元,请选出最省线的租车方案,并求出最少租金.
参考答案:
【答案】(1)1辆小客车坐20人,1辆大客车坐45人;
(2)①3种租车方案。①分别是租小车20辆,不租大车;②租小车11辆,租大车4辆;③租小车2辆,租大车8辆;
②方案3最省钱,需要3300元。
【解析】分析:(1)设每辆小客车能坐x人,每辆大客车能坐y人,根据题意可得等量关系:3辆小客车座的人数+1辆大客车座的人数=105人;1辆小客车座的人数+2辆大客车座的人数=110人,根据等量关系列出方程组,再解即可;(2)①根据题意可得小客车m辆运的人数+大客车n辆运的人数=400,然后求出整数解即可;②根据①所得方案和小客车每辆租金150元,大客车每辆租金250元分别计算出租金即可.
本题解析:
(1)设1辆小客车一次可送学生x人,1辆大客车都坐满后一次可送y名学生,
由题意得: ![]()
解得: ![]()
答:1辆小客车坐20人,1辆大客车坐45人。
(2)设租小客车a辆,大客车b辆,由题意得:
20a+45b=400,
∵每辆汽车恰好都坐满,
∴a、b的值均为非负整数,
∴a、b可取![]() ,
, ![]() ,
, ![]()
答:共有3种租车方案。①分别是租小车20辆,不租大车;②租小车11辆,租大车4辆;③租小车2辆,租大车8辆;
(3)方案1租金为:250×20=5000(元);
方案2租金为:250×11+350×4=4150(元);
方案3租金为:250×2+350×8=3300(元).
答,方案3最省钱,需要3300元。
点睛:本题主要考查了二元一次方程组的应用,二元一次方程的应用,关键是准确理解题意,找出题目中的等量关系,列出二元一次方程或方程组.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数-6,-2,-3,-1.2中,最大的负整数的是( )
A. 0 B. -2 C. -3 D. -1.2
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P在四象限,且点P到x轴的距离为3,点P到y轴的距离为2,则点P的坐标为( )
A.(﹣3,﹣2)
B.(3,﹣2)
C.(2,3)
D.(2,﹣3) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点N,连接BM,DN.

(1)求证:四边形BMDN是菱形;
(2)若AB=4,AD=8,求MD的长
-
科目: 来源: 题型:
查看答案和解析>>【题目】(6分)在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复,表是活动进行中的一组统计数据:
摸球的次数n
100
150
200
500
800
1000
摸到白球的次数m
68
109
136
345
368
701
摸到乒乓球的频率
0.68
0.73
0.68
0.69
0.70
0.70
(1)请估计:当n很大时,摸到白球的频率将会接近________;
(2)假如你去摸一次,你摸到白球的概率是_______,摸到黑球的概率是_______;
(3)试估算口袋中黑、白两种颜色的球各有多少只?
-
科目: 来源: 题型:
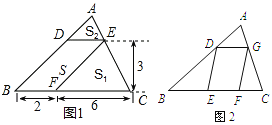
查看答案和解析>>【题目】问题背景(1)如图1,△ABC中,DE∥BC分别交AB,AC于D,E两点,过点E作EF∥AB交BC于点F.请按图示数据填空:△EFC的面积
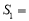 __________,△ADE的面积
__________,△ADE的面积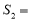 ______________.
______________.探究发现(2)在(1)中,若BF=m,FC=n,DE与BC间的距离为
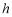 .请证明
.请证明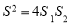 .
.拓展迁移(3)如图2,□DEFG的四个顶点在△ABC的三边上,若△ADG、△DBE、△GFC的面积分别为3、7、5,试利用(2)中的结论求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点A(0,1)、D(-2,0),作直线AD并以线段AD为一边向上作正方形ABCD.
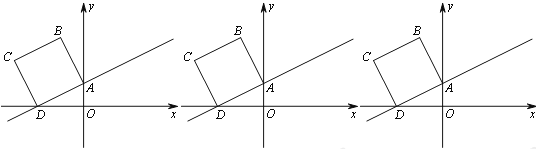
(1)填空:点B的坐标为________,点C的坐标为_________.
(2)若正方形以每秒
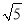 个单位长度的速度沿射线DA向上平移,直至正方形的顶点C落在y轴上时停止运动.在运动过程中,设正方形落在y轴右侧部分的面积为S,求S关于平移时间t(秒)的函数关系式,并写出相应的自变量t的取值范围.
个单位长度的速度沿射线DA向上平移,直至正方形的顶点C落在y轴上时停止运动.在运动过程中,设正方形落在y轴右侧部分的面积为S,求S关于平移时间t(秒)的函数关系式,并写出相应的自变量t的取值范围.
相关试题

