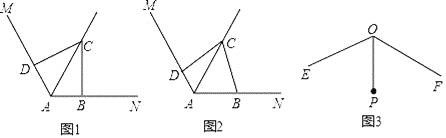
【题目】已知∠MAN=120°,点C是∠MAN的平分线AQ上的一个定点,点B,D分别在AN,AM上,连接BD.
【发现】
(1)如图1,若∠ABC=∠ADC=90°,则∠BCD= °,△CBD是 三角形;
【探索】
(2)如图2,若∠ABC+∠ADC=180°,请判断△CBD的形状,并证明你的结论;
【应用】
(3)如图3,已知∠EOF=120°,OP平分∠EOF,且OP=1,若点G,H分别在射线OE,OF上,且△PGH为等边三角形,则满足上述条件的△PGH的个数一共有 .(只填序号)
①2个②3个③4个④4个以上
参考答案:
【答案】(1)60,等边;(2)等边三角形,证明见解析(3)④.
【解析】试题分析:(1)利用四边形的内角和即可得出∠BCD的度数,再利用角平分线的性质定理即可得出CB,即可得出结论;
(2)先判断出∠CDE=∠ABC,进而得出△CDE≌△CFB(AAS),得出CD=CB,再利用四边形的内角和即可得出∠BCD=60°即可得出结论;
(3)先判断出∠POE=∠POF=60°,先构造出等边三角形,找出特点,即可得出结论.
试题解析:(1)如图1,连接BD,
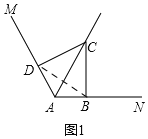
∵∠ABC=∠ADC=90°,∠MAN=120°,
根据四边形的内角和得,∠BCD=360°-(∠ABC+∠ADC+∠MAN)=60°,
∵AC是∠MAN的平分线,CD⊥AM.CB⊥AN,
∴CD=CB,(角平分线的性质定理),
∴△BCD是等边三角形;
故答案为:60,等边;
(2)如图2,同(1)得出,∠BCD=60°(根据三角形的内角和定理),
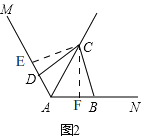
过点C作CE⊥AM于E,CF⊥AN于F,
∵AC是∠MAN的平分线,
∴CE=CF,
∵∠ABC+∠ADC=180°,∠ADC+∠CDE=180°,
∴∠CDE=∠ABC,
在△CDE和△CFB中,
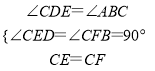 ,
,
∴△CDE≌△CFB(AAS),
∴CD=CB,
∵∠BCD=60°,
∴△CBD是等边三角形;
(3)如图3,
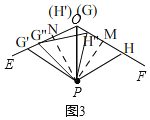
∵OP平分∠EOF,∠EOF=120°,
∴∠POE=∠POF=60°,在OE上截取OG'=OP=1,连接PG',
∴△G'OP是等边三角形,此时点H'和点O重合,
同理:△OPH是等边三角形,此时点G和点O重合,
将等边△PHG绕点P逆时针旋转到等边△PG'H',在旋转的过程中,
边PG,PH分别和OE,OF相交(如图中G',H')和点P围成的三角形全部是等边三角形,(旋转角的范围为(0°到60°包括0°和60°),
所以有无数个;
理由:同(2)的方法.
故答案为④.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,A(-1,5),B(-1,0),C(-4,3).
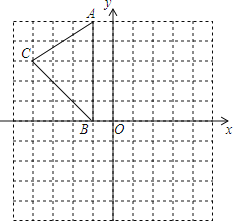
(1)在图中作出△ABC关于y轴的对称图形△A1B1C1;
(2)写出点A1、B1、C1的坐标;
(3)在y轴上画出点P,使PA+PC最小;
(4)求六边形AA1C1B1BC的面积.. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙、丙三个登山爱好者经常相约去登山,今年1月甲参加了两次登山活动.
(1)1月1日甲与乙同时开始攀登一座900米高的山,甲的平均攀登速度是乙的1.2倍,结果甲比乙早15分钟到达顶峰.求甲的平均攀登速度是每分钟多少米?
(2)1月6日甲与丙去攀登另一座h米高的山,甲保持第(1)问中的速度不变,比丙晚出发0.5小时,结果两人同时到达顶峰,问甲的平均攀登速度是丙的多少倍?(用含h的代数式表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数图象的顶点坐标是(-1,2),且过点(0,
 ).
).(1)求二次函数的解析式,并在图中画出它的图象;
(2)求证:对任意实数m,点M(m,-m2)都不在这个二次函数的图象上.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将长方形纸片ABCD折叠,使边DC落在对角线AC上,折痕为CE,且D点落在对角线D′处.若AB=3,AD=4,则ED的长为( )

A.
 B. 3 C. 1 D.
B. 3 C. 1 D. 
-
科目: 来源: 题型:
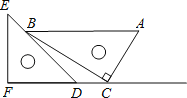
查看答案和解析>>【题目】一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10,试求CD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,折叠长方形一边AD,点D落在BC边的点F处,BC=10cm,AB=8cm。

求:(1)FC的长;
(2)EF的长。
相关试题

