【题目】在平面直角坐标系中,一次函数y=kx+b的图象与x轴、y轴分别相交于A(﹣3,0),B(0,﹣3)两点,二次函数y=x2+mx+n的图象经过点A.
(1)求一次函数y=kx+b的解析式;
(2)若二次函数y=x2+mx+n图象的顶点在直线AB上,求m,n的值;
(3)当﹣3≤x≤0时,二次函数y=x2+mx+n的最小值为﹣4,求m,n的值.
参考答案:
【答案】
(1)
解:A(﹣3,0),B(0,﹣3)代入y=kx+b得
![]() ,解得
,解得 ![]() ,
,
∴一次函数y=kx+b的解析式为:y=﹣x﹣3
(2)
解:二次函数y=x2+mx+n图象的顶点为(﹣ ![]() ,
, ![]() )
)
∵顶点在直线AB上,
∴ ![]() =
= ![]() ﹣3,
﹣3,
又∵二次函数y=x2+mx+n的图象经过点A(﹣3,0),
∴9﹣3m+n=0,
∴组成方程组为 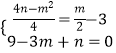
解得 ![]() 或
或 ![]()
(3)
解:∵二次函数y=x2+mx+n的图象经过点A.
∴9﹣3m+n=0,
∵当﹣3≤x≤0时,二次函数y=x2+mx+n的最小值为﹣4,
①如图1,当对称轴﹣3<﹣ ![]() <0时
<0时

最小值为 ![]() =﹣4,与9﹣3m+n=0,组成方程组为
=﹣4,与9﹣3m+n=0,组成方程组为
 解得
解得 ![]() 或
或 ![]() (由﹣3<﹣
(由﹣3<﹣ ![]() <0知不符合题意舍去)
<0知不符合题意舍去)
所以 ![]() .
.
②如图2,当对称轴﹣ ![]() >0时,在﹣3≤x≤0时,x为0时有最小值为﹣4,
>0时,在﹣3≤x≤0时,x为0时有最小值为﹣4,

把(0,﹣4)代入y=x2+mx+n得n=﹣4,
把n=﹣4代入9﹣3m+n=0,得m= ![]() .
.
∵﹣ ![]() >0,
>0,
∴m<0,
∴此种情况不成立,
③当对称轴﹣ ![]() =0时,y=x2+mx+n的最小值为﹣4,
=0时,y=x2+mx+n的最小值为﹣4,
把(0,﹣4)代入y=x2+mx+n得n=﹣4,
把n=﹣4代入9﹣3m+n=0,得m= ![]() .
.
∵﹣ ![]() =0,
=0,
∴m=0,
∴此种情况不成立,
④当对称轴﹣ ![]() ≤﹣3时,最小值为0,不成立
≤﹣3时,最小值为0,不成立
综上所述m=2,n=﹣3.
【解析】(1)利用待定系数法求出解析式,(2)先表示出二次函数y=x2+mx+n图象的顶点,利用直线AB列出式子,再与点A在二次函数上得到的式子组成方程组求得m,n的值,(3)本题要分四种情况①当对称轴﹣3<﹣ ![]() <0时,②当对称轴﹣
<0时,②当对称轴﹣ ![]() >0时,③当对称轴﹣
>0时,③当对称轴﹣ ![]() =0时,④当对称轴﹣
=0时,④当对称轴﹣ ![]() ≤﹣3时,结合二次函数y=x2+mx+n的图象经过点A得出的式子9﹣3m+n=0,求出m,n但一定要验证是否符合题意.
≤﹣3时,结合二次函数y=x2+mx+n的图象经过点A得出的式子9﹣3m+n=0,求出m,n但一定要验证是否符合题意.
【考点精析】本题主要考查了二次函数的性质的相关知识点,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】中国“蛟龙”号深潜器目前最大深潜极限为7062.68米.如图,某天该深潜器在海面下2000米的A点处作业,测得俯角为30°正前方的海底C点处有黑匣子信号发出.该深潜器受外力作用可继续在同一深度直线航行3000米后,再次在B点处测得俯角为45°正前方的海底C点处有黑匣子信号发出,请通过计算判断“蛟龙”号能否在保证安全的情况下打捞海底黑匣子.(参考数据
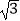 ≈1.732)
≈1.732)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的布袋里装有4个标有1,2,3,4的小球,它们的形状、大小、质地完全相同,小李从布袋里随机取出一个小球,记下数字为x,小张在剩下的3个小球中随机取出一个小球,记下数字为y,这样确定了点Q的坐标(x,y).
(1)画树状图或列表,写出点Q所有可能的坐标;
(2)求点Q(x,y)在函数y=﹣x+5图象上的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BD为⊙O的直径,AB=AC,AD交BC于点E,AE=1,ED=2.

(1)求证:∠ABC=∠D;
(2)求AB的长;
(3)延长DB到F,使得BF=BO,连接FA,试判断直线FA与⊙O的位置关系,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,A(1,1),B(﹣1,1),C(﹣1,﹣2),D(1,﹣2).把一条长为2014个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A﹣B﹣C﹣D﹣A…的规律绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是( )

A.(﹣1,0)
B.(1,﹣2)
C.(1,1)
D.(﹣1,﹣1) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A(4,0),B(3,3),以AO,AB为边作平行四边形OABC,则经过C点的反比例函数的解析式为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(
 )﹣1﹣20140﹣2sin30°+
)﹣1﹣20140﹣2sin30°+ 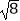 .
.
相关试题

