【题目】如图,BD为⊙O的直径,AB=AC,AD交BC于点E,AE=1,ED=2. 
(1)求证:∠ABC=∠D;
(2)求AB的长;
(3)延长DB到F,使得BF=BO,连接FA,试判断直线FA与⊙O的位置关系,并说明理由.
参考答案:
【答案】
(1)证明:∵AB=AC,
∴∠ABC=∠C,
∵∠C与∠D所对应的弧均为 ![]() ,
,
∴∠C=∠D,
∴∠ABC=∠D
(2)解:∵∠ABC=∠D,∠BAE=∠DAB,
∴△ABE∽△ADB,
∴ ![]() ,
,
即AB2=AE(AE+ED)=3,
解得:AB= ![]()
(3)答:直线FA与⊙O相切.理由如下:
连接OA,

∵BD为⊙O的直径,
∴∠BAD=90°,
在Rt△ABD中,AB= ![]() ,AD=1+2=3,
,AD=1+2=3,
根据勾股定理得:BD=2 ![]() ,
,
∴OB=OA=AB= ![]() ,
,
∵BF=OB,
∴AB=FB=OB,即AB= ![]() OF,
OF,
∴∠OAF=90°,
则直线AF与⊙O相切.
【解析】(1)由AB=AC,利用等边对等角得到∠ABC=∠C,再由同弧所对的圆周角相等得到∠C=∠D,等量代换即可得证;(2)由(1)的结论与公共角相等,得到△ABE与△ADB相似,由相似得比例,即可求出AB的长;(3)直线FA与⊙O相切,理由为:连接OA,由BD为直径,得到∠BAD为直角,在Rt△ABD中,利用勾股定理求出BD的长,得到AB=OB=OA,根据BF=BO,得到AB等于FO的一半,确定出∠OAF为直角,即可得证.
【考点精析】本题主要考查了圆周角定理和切线的判定定理的相关知识点,需要掌握顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半;切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,对角线AC,BD相交于点O,且AC⊥BD,点E,F,G,H分别是AB,BC,CD,DA的中点,依次连接各边中点得到四边形EFGH,求证:四边形EFGH是矩形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】中国“蛟龙”号深潜器目前最大深潜极限为7062.68米.如图,某天该深潜器在海面下2000米的A点处作业,测得俯角为30°正前方的海底C点处有黑匣子信号发出.该深潜器受外力作用可继续在同一深度直线航行3000米后,再次在B点处测得俯角为45°正前方的海底C点处有黑匣子信号发出,请通过计算判断“蛟龙”号能否在保证安全的情况下打捞海底黑匣子.(参考数据
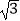 ≈1.732)
≈1.732)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的布袋里装有4个标有1,2,3,4的小球,它们的形状、大小、质地完全相同,小李从布袋里随机取出一个小球,记下数字为x,小张在剩下的3个小球中随机取出一个小球,记下数字为y,这样确定了点Q的坐标(x,y).
(1)画树状图或列表,写出点Q所有可能的坐标;
(2)求点Q(x,y)在函数y=﹣x+5图象上的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,一次函数y=kx+b的图象与x轴、y轴分别相交于A(﹣3,0),B(0,﹣3)两点,二次函数y=x2+mx+n的图象经过点A.

(1)求一次函数y=kx+b的解析式;
(2)若二次函数y=x2+mx+n图象的顶点在直线AB上,求m,n的值;
(3)当﹣3≤x≤0时,二次函数y=x2+mx+n的最小值为﹣4,求m,n的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,A(1,1),B(﹣1,1),C(﹣1,﹣2),D(1,﹣2).把一条长为2014个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A﹣B﹣C﹣D﹣A…的规律绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是( )

A.(﹣1,0)
B.(1,﹣2)
C.(1,1)
D.(﹣1,﹣1) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A(4,0),B(3,3),以AO,AB为边作平行四边形OABC,则经过C点的反比例函数的解析式为 .

相关试题

