【题目】某数学兴趣小组利用大小不等、颜色各异的正方形硬纸片开展了一次活动,请认真阅读下面的探究片段,完成所提出的问题。
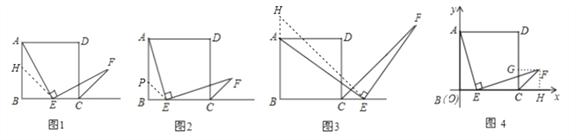
探究1:四边形ABCD是边长为1正方形,点E是边BC的中点,∠AEF=90°,且EF交正方形外角的平分线CF于点F,小明看到图(1)后,很快发现AE=EF,这需要证明AE与EF所在的两个三角形全等,但△ABE与△FCE显然不全等,考虑到点E是BC的中点,引条辅助线尝试就行了,随即小明写出了如下的证明过程:证明:取AB的中点H,连接EH,证明△AHE与△ECF全等即可.
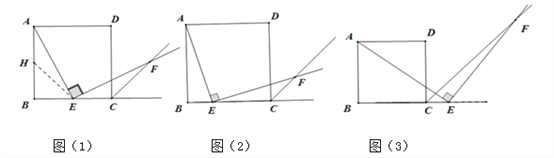
探究2:小明继续探索,把条件“点E是边BC的中点”改为“点E是边BC上的任意一点”,如图(2)其它条件不变,结论AE=EF是否成立呢? (填是或否)
小明还想试试,把条件“点E是边BC的中点”改为“点E是边BC延长线上的任意一点”,如图(3)其它条件不变,那么结论AE=EF是否还成立呢? (填是或否),请你选择其中一种完成证明过程给小强看。
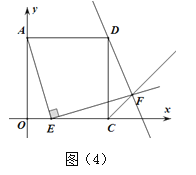
探究3:在探究2结论AE=EF成立的情况下,如图(4)所示的平面直角坐标系中,当点E滑动到BC上某处时(不含B、C),点F恰好落在直线y=-2x+3上,求此时点F的坐标.
参考答案:
【答案】 (1)见解析;(2) F(![]() ,
,![]() ).
).
【解析】分析:探究1:取AB的中点H,连接EH,根据同角的余角相等得到∠BAE=∠CEF,证明△HAE≌△CEF即可;
探究2:①在AB上取点P,连接EP,同(1)的方法相似,证明△PAE≌△CEF即可;
②延长BA至H,使AH=CE,连接HE,证明△HAE≌△CEF即可.
探究3:设F(a,﹣2a+3),过F作FH⊥x轴于H,作FG⊥CD于G,如图4,只要证明FG=FH,由此构建方程即可解决问题;
详解:探究1:如图1,取AB的中点H,连接EH.
∵四边形ABCD是正方形,
∴AB=BC,∠B=∠BCD=90°.
∵AH=EC,∴BH=BE,∴∠BHE=45°,∠AHE=135°.
∵CF是正方形外角的平分线,∴∠ECF=135°.
∵∠AEF=90°,∠B=90°,∴∠BAE=∠CEF.
在△HAE和△CEF中,∵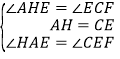 ,∴△HAE≌△CEF,∴AE=EF;
,∴△HAE≌△CEF,∴AE=EF;
探究2:①结论:是.
理由:如图2,在AB上取点P,连接EP.
∵四边形ABCD是正方形,∴AB=BC,∠B=∠BCD=90°.
∵AP=EC,∴BP=BE,∴∠BPE=45°,∠APE=135°.
∵CF是正方形外角的平分线,∴∠ECF=135°.
∵∠AEF=90°,∠B=90°,∴∠BAE=∠CEF.在△PAE和△CEF中,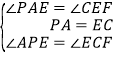 ,∴△PAE≌△CEF,∴AE=EF;
,∴△PAE≌△CEF,∴AE=EF;
②结论:是.
理由:如图3,延长BA至H,使AH=CE,连接HE.
∵BA=BC,AH=CE,∴BH=BE,∴∠H=45°.
∵CF是正方形外角的平分线,∴∠ECF=45°,∴∠H=∠ECF.
∵∠AEF=90°,∠B=90°,∠HAE=∠B+∠BEA,∠CEF=∠AEF+∠BEA,
∴∠HAE=∠CEF.
在△HAE和△CEF中,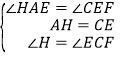 ,∴△HAE≌△CEF,∴AE=EF.
,∴△HAE≌△CEF,∴AE=EF.
探究3:②设F(a,﹣2a+3),过F作FH⊥x轴于H,作FG⊥CD于G,如图4,
则CH=a﹣1,FH=﹣2a+3.
∵CF为角平分线,∴FH=CH,∴a﹣1=﹣2a+3,解得:a=![]() .当a=
.当a=![]() 时,﹣2a+3=﹣2×
时,﹣2a+3=﹣2×![]() +3=
+3=![]() ,∴F点坐标为(
,∴F点坐标为(![]() ).
).
-
科目: 来源: 题型:
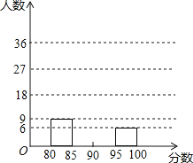
查看答案和解析>>【题目】某校举办“红歌伴我成长”歌咏比赛活动,参赛同学的成绩分别绘制成频数分布表和频数分布直方图(均不完整)如图:
分数段
频数
频率
80≤x<85
9
0.15
85≤x<90
m
0.45
90≤x<95
■
■
95≤x<100
6
n
(1)求m,n的值分别是多少;
(2)请在图中补全频数分布直方图;
(3)比赛成绩的中位数落在哪个分数段?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在数轴上点A表示数a,点B表示数b,点C表示数c,a是多项式2x24x+1的一次项系数,b是最小的正整数,单项式
 x2y4的次数为c.
x2y4的次数为c.
(1)a=___,b=___,c=___;
(2)若将数轴在点B处折叠,则点A与点C___重合(填“能”或“不能”);
(3)点A,B,C开始在数轴上运动,若点C以每秒1个单位长度的速度向右运动,同时,点A和点B分别以每秒3个单位长度和2个单位长度的速度向左运功,t分钟过后,若点A与点B之间的距离表示为AB,点B与点C之间的距离表示为BC,则AB=___,BC=___(用含t的代数式表示);
(4)请问:3ABBC的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值。
-
科目: 来源: 题型:
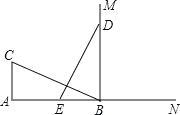
查看答案和解析>>【题目】如图,CA⊥AB,垂足为 A,AB=24,AC=12,射线 BM⊥AB,垂足为 B, 一动点 E 从 A点出发以 3 厘米/秒沿射线 AN 运动,点 D 为射线 BM 上一动点, 随着 E 点运动而运动,且始终保持 ED=CB,当点 E 经过______秒时,△DEB 与△BCA 全等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】这是一根起点为0的数轴,现有同学将它弯折,如图所示, 例如:虚线上第一行0,第二行6,第三行21…,第9行的数是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 ,O是AC上的一点,
,O是AC上的一点,  与BC,AB分别切于点C,D, 与AC相交于点E,连接BO.
与BC,AB分别切于点C,D, 与AC相交于点E,连接BO.(1) 求证:CE2=2DE
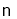 BO;
BO;(2) 若BC=CE=6,则AE= ,AD= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD中,∠B=90°,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积为______。

相关试题

