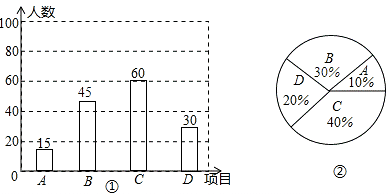
【题目】为推广阳光体育“大课间”活动,某中学决定在学生中开设A:实心球,B:立定跳远,C:跳绳,D:跑步四种活动项目,为了了解学生对四种项目的喜欢情况,随机抽取了部分学生进行调查,并将调查结果绘制成如图①②的统计图.请结合图中的信息解答下列问题: 
(1)在这项调查中,共调查了多少名学生?
(2)请计算喜欢“立定跳远”的学生人数和所占百分比,并将两个统计图补充完整;
(3)若调查到喜欢“跳绳”的4名学生中有2名男生,2名女生.现从这4名学生中任意抽取2名学生.请用画树状图或列表的方法,求出刚好抽到同性别学生的概率.
参考答案:
【答案】
(1)解:15÷10%=150(名),
答;在这项调查中,共调查了150名学生
(2)解:本项调查中喜欢“立定跳远”的学生人数=150﹣15﹣60﹣30=45(人),
它所占百分比= ![]() ×100%=30%,
×100%=30%,
画图如下:
(3)解:画树状图为:
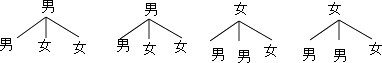
共有12种等可能的结果数,其中相同性别的学生的结果数为4,
所以相同性别的学生的概率= ![]() =
= ![]()
【解析】(1)用A类人数除以它所占百分比即可得到调查的总人数;(2)用总人数分别减去A、C、D类人数即可得到B类人数,再计算B类所占百分比,然后补全统计图;(3)用A表示男生,B表示女生,先画树状图展示所有12种等可能的结果数,再找出到同性别学生的结果数,然后根据概率公式求解.
【考点精析】认真审题,首先需要了解扇形统计图(能清楚地表示出各部分在总体中所占的百分比.但是不能清楚地表示出每个项目的具体数目以及事物的变化情况),还要掌握条形统计图(能清楚地表示出每个项目的具体数目,但是不能清楚地表示出各个部分在总体中所占的百分比以及事物的变化情况)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】因市场竞争激烈,国商进行促销活动,决定对学习用品进行打八折出售,打折前,买2本笔记本和1支圆珠笔需要18元,买1本笔记本和2支圆珠笔需要12元.
(1)求打折前1本笔记本,1支圆珠笔各需要多少元.
(2)在促销活动时间内,购买50本笔记本和40支圆珠笔共需要多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,已知点A(﹣1,2),B(﹣2,0),C(﹣4,1),把三角形ABC向上平移1个单位长度,向右平移5个单位长度,可以得到三角形A′B′C′.
(Ⅰ)在图中画出△A′B′C′;
(Ⅱ)直接写出点A′、B′、C′的坐标;
(Ⅲ)写出A′C′与AC之间的位置关系和大小关系.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了考察某种大麦细长的分布情况,在一块试验田里抽取了部分麦穗.测得它们的长度,数据整理后的频数分布表及频数分直方图如下.根据以下信息,解答下列问题:
穗长x
频数
4.0≤x<4.3
1
4.3≤x<4.6
1
4.6≤x<4.9
2
4.9≤x<5.2
5
5.2≤x<5.5
11
5.5≤x<5.8
15
5.8≤x<6.1
28
6.1≤x<6.4
13
6.4≤x<6.7
11
6.7≤x<7.0
10
7.0≤x<7.3
2
7.3≤x<7.6
1
(Ⅰ)补全直方图;
(Ⅱ)共抽取了麦穗 棵;
(Ⅲ)频数分布表的组距是 ,组数是 ;
(Ⅳ)麦穗长度在5.8≤x<6.1范围内麦穗有多少棵?占抽取麦穗的百分之几?
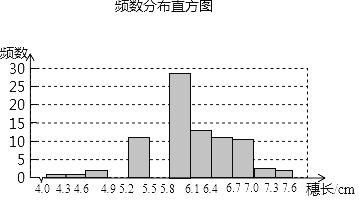
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:

(1)如图(1),等边△ABC内有一点P到顶点A,B,C的距离分别为3,4,5,则∠APB= .
分析:由于PA,PB不在一个三角形中,为了解决本题我们可以将△ABP绕顶点A旋转到△ACP′处,此时△ACP′≌ , 这样,就可以利用全等三角形知识,将三条线段的长度转化到一个三角形中从而求出∠APB的度数.
(2)请你利用第(1)题的解答思想方法,解答下面问题:已知如图(2),△ABC中,∠CAB=90°,AB=AC,E、F为BC上的点且∠EAF=45°,求证:BE2+CF2=EF2 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=kx+b的图象经过点(-1,-5),且与正比例函数y=
 x的图象相交于点(2,a),求:
x的图象相交于点(2,a),求:(1)a的值.
(2)k,b的值.
(3)这两个函数图象与x轴所围成的三角形的面积。

-
科目: 来源: 题型:
查看答案和解析>>【题目】某汽车专买店销售A,B两种型号的新能源汽车,上周售出1辆A型车和3辆B型车,销售额为96万元;本周已售出2辆A型车和1辆B型车,销售额为62万元.
(1)求每辆A型车和B型车的件价各为多少万元;
每辆A型车和B型车的售价分别是x万元,y万元.
根据题意,列方程组
解这个方程组,得x= ,y=
答: .
(2)有一家公司拟向该店购买A,B两种型号的新能源汽车共6辆,购车费不超过130万元,求这次购进B型车最多几辆?
相关试题

