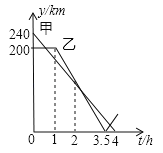
【题目】在一条笔直的公路上有A、B、C三地,C地位于A、B两地之间,甲车从A地沿这条公路匀速驶向C地,乙车从B地沿这条公路匀速驶向A地,在甲车出发至甲车到达C地的过程中,甲、乙两车各自与C地的距离y(km)与甲车行驶时间t(h)之间的函数关系如图所示.下列结论:①甲车出发2h时,两车相遇;②乙车出发1.5h时,两车相距170km;③乙车出发![]() h时,两车相遇;④甲车到达C地时,两车相距40km.其中正确的是______(填写所有正确结论的序号).
h时,两车相遇;④甲车到达C地时,两车相距40km.其中正确的是______(填写所有正确结论的序号).
参考答案:
【答案】②③④.
【解析】解:①观察函数图象可知,当t=2时,两函数图象相交,∵C地位于A、B两地之间,∴交点代表了两车离C地的距离相等,并不是两车相遇,结论①错误;
②甲车的速度为240÷4=60(km/h),乙车的速度为200÷(3.5﹣1)=80(km/h),∵(240+200﹣60﹣170)÷(60+80)=1.5(h),∴乙车出发1.5h时,两车相距170km,结论②正确;
③∵(240+200﹣60)÷(60+80)=![]() (h),∴乙车出发
(h),∴乙车出发![]() h时,两车相遇,结论③正确;
h时,两车相遇,结论③正确;
④∵80×(4﹣3.5)=40(km),∴甲车到达C地时,两车相距40km,结论④正确.
综上所述,正确的结论有:②③④.
故答案为:②③④.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A在CB的延长线上,点F在DE的延长线上,连接AF,分别与BD、CE交于点G、H。已知∠1=52°,∠2=128°。
(1)求证:BD∥CE;
(2)若∠A=∠F,试判断∠C与∠D的数量关系,并说明理由。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形
 中,对角线
中,对角线 、
、 相交于点
相交于点 .
.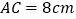 ,
,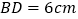 ,点
,点 为
为 上一动点,点
上一动点,点 以
以 的速度从点
的速度从点 出发沿
出发沿 向点
向点 运动.设运动时间为
运动.设运动时间为 ,当
,当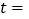 ________
________ 时,
时, 为等腰三角形.
为等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在菱形ABCD中,F为边BC的中点,DF与对角线AC交于点M,过M作ME⊥CD于点E,∠1=∠2.
(1)若CE=1,求BC的长;
(2)求证:AM=DF+ME.

-
科目: 来源: 题型:
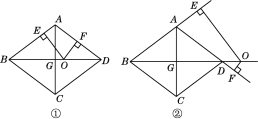
查看答案和解析>>【题目】如图,在边长为10的菱形ABCD中,对角线BD=16,对角线AC,BD相交于点G,点O是直线BD上的动点,OE⊥AB于E,OF⊥AD于F.
(1)求对角线AC的长及菱形ABCD的面积.
(2)如图①,当点O在对角线BD上运动时,OE+OF的值是否发生变化?请说明理由.
(3)如图②,当点O在对角线BD的延长线上时,OE+OF的值是否发生变化?若不变,请说明理由;若变化,请探究OE,OF之间的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学习了乘法公式
 后,老师向同学们提出了如下问题:
后,老师向同学们提出了如下问题:①将多项式x2+4x+3因式分解;
②求多项式x2+4x+3的最小值.

请你运用上述的方法解决下列问题:
(1)将多项式x2+8x-20因式分解;
(2)求多项式x2+8x-20的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司有A、B两种型号的客车共20辆,它们的载客量、每天的租金如表所示.已知在20辆客车都坐满的情况下,共载客720人.
A型号客车
B型号客车
载客量(人/辆)
45
30
租金(元/辆)
600
450
(1)求A、B两种型号的客车各有多少辆?
(2)某中学计划租用A、B两种型号的客车共8辆,同时送七年级师生到沙家浜参加社会实践活动,已知该中学租车的总费用不超过4600元.
①求最多能租用多少辆A型号客车?
②若七年级的师生共有305人,请写出所有可能的租车方案,并确定最省钱的租车方案.
相关试题

