【题目】如图,在菱形![]() 中,对角线
中,对角线![]() 、
、![]() 相交于点
相交于点![]() .
.![]() ,
,![]() ,点
,点![]() 为
为![]() 上一动点,点
上一动点,点![]() 以
以![]() 的速度从点
的速度从点![]() 出发沿
出发沿![]() 向点
向点![]() 运动.设运动时间为
运动.设运动时间为![]() ,当
,当![]() ________
________![]() 时,
时,![]() 为等腰三角形.
为等腰三角形.

参考答案:
【答案】![]() 或
或![]() 或
或![]()
【解析】
求出BA的值,根据已知画出符合条件的三种情况:①当PA=AB=5cm时,②当P和C重合时,PB=AB=5cm,③作AB的垂直平分线交AC于P,此时PB=PA,连接PB,求出即可.
∵四边形ABCD是菱形,AC=8cm,BD=6cm,
∴AC⊥BD,AO=OC=4cm,BO=OD=3cm,
由勾股定理得:BC=AB=AD=CD=5cm,
分为三种情况:①如图1,当PA=AB=5cm时,t=5÷1=5(s);

②如图2,当P和C重合时,PB=AB=5cm,t=8÷1=8(s);
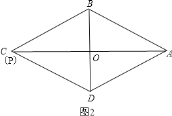
③如图3,作AB的垂直平分线交AC于P,此时PB=PA,连接PB,
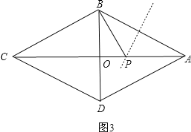
在Rt△BOP中,由勾股定理得:BP2=BO2+OP2,
AP2=32+(4-AP)2,
AP=![]() ,
,
t=![]() ÷1=
÷1=![]() (s),
(s),
故答案为:5或8或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)每年的6月5日为世界环保日,为提倡低碳环保,某公司决定购买10台节省能源的新机器,现有甲、乙两种型号的新机器可选,其中每台的价格、工作量如下表.
甲型机器
乙型机器
价格(万元/台)
a
b
产量(吨/月)
240
180
经调查:购买一台甲型机器比购买一台乙型机器多2万元,购买2台甲型机器比购买3台乙型机器少6万元.
(1)求a、b的值;
(2)若该公司购买新机器的资金不能超过110万元,请问该公司有几种购买方案?
(3)在(2)的条件下,若公司要求每月的产量不低于2040吨,请你为该公司设计一种最省钱的购买方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在四边形ABCD中,∠A=x°,∠C=y°(0°<x<180°,0°<y<180°).
(1)∠ABC+∠ADC= °.(用含x,y的代数式表示)
(2)如图1,若x=y=90°,DE平分∠ADC,BF平分与∠ABC相邻的外角,请写出DE与BF的位置关系,并说明理由.
(3)如图2,∠DFB为四边形ABCD的∠ABC、∠ADC相邻的外角平分线所在直线构成的锐角,
①当x<y时,若x+y=140°,∠DFB=30°,试求x、y.
②小明在作图时,发现∠DFB不一定存在,请直接指出x、y满足什么条件时,∠DFB不存在.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A在CB的延长线上,点F在DE的延长线上,连接AF,分别与BD、CE交于点G、H。已知∠1=52°,∠2=128°。
(1)求证:BD∥CE;
(2)若∠A=∠F,试判断∠C与∠D的数量关系,并说明理由。

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在菱形ABCD中,F为边BC的中点,DF与对角线AC交于点M,过M作ME⊥CD于点E,∠1=∠2.
(1)若CE=1,求BC的长;
(2)求证:AM=DF+ME.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在一条笔直的公路上有A、B、C三地,C地位于A、B两地之间,甲车从A地沿这条公路匀速驶向C地,乙车从B地沿这条公路匀速驶向A地,在甲车出发至甲车到达C地的过程中,甲、乙两车各自与C地的距离y(km)与甲车行驶时间t(h)之间的函数关系如图所示.下列结论:①甲车出发2h时,两车相遇;②乙车出发1.5h时,两车相距170km;③乙车出发
 h时,两车相遇;④甲车到达C地时,两车相距40km.其中正确的是______(填写所有正确结论的序号).
h时,两车相遇;④甲车到达C地时,两车相距40km.其中正确的是______(填写所有正确结论的序号).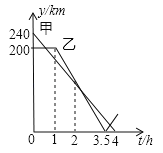
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为10的菱形ABCD中,对角线BD=16,对角线AC,BD相交于点G,点O是直线BD上的动点,OE⊥AB于E,OF⊥AD于F.
(1)求对角线AC的长及菱形ABCD的面积.
(2)如图①,当点O在对角线BD上运动时,OE+OF的值是否发生变化?请说明理由.
(3)如图②,当点O在对角线BD的延长线上时,OE+OF的值是否发生变化?若不变,请说明理由;若变化,请探究OE,OF之间的数量关系.
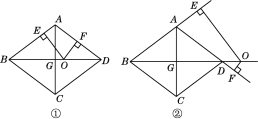
相关试题

