【题目】如图,O为直线AB上一点,OD平分∠AOC,∠DOE=90°.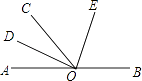
(1)若∠AOC=50°,求出∠BOD的度数;
(2)试判断OE是否平分∠BOC,并说明理由.
参考答案:
【答案】
(1)解:因为∠AOC=50°,OD平分∠AOC,
所以∠DOC= ![]() ∠AOC=25°,∠BOC=180°﹣∠AOC=130°,
∠AOC=25°,∠BOC=180°﹣∠AOC=130°,
所以∠BOD=∠DOC+∠BOC=155°;
(2)解:OE平分∠BOC.理由如下:
∵OD平分∠AOC,
∴∠DOA=∠DOC,
∵∠DOE=90°,
∴∠DOC+∠COE=90°,∠DOA+∠BOE=90°,
∴∠COE=∠BOE,
∴OE平分∠BOC.
【解析】(1)根据角平分线的定义知∠DOC的度数,然后根据邻补角的定义得出∠BOC的度数,然后根据∠BOD=∠DOC+∠BOC算出答案;
(2)根据角平分线的定义得出∠DOA=∠DOC,再根据等角的余角相等得出答案。
【考点精析】本题主要考查了角的平分线判定和余角和补角的特征的相关知识点,需要掌握可以证明三角形内存在一个点,它到三角形的三边的距离相等这个点就是三角形的三条角平分线的交点(交于一点);互余、互补是指两个角的数量关系,与两个角的位置无关才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中正确的是( )
A.矩形的对角线一定垂直B.对角线互相垂直平分的四边形是正方形
C.四个角都相等的四边形是正方形D.菱形的对角线互相垂直平分
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知Rt△ABC中,斜边AB=10cm,则斜边上的中线的长为______.
-
科目: 来源: 题型:
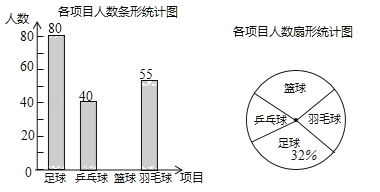
查看答案和解析>>【题目】某学校准备开展“阳光体育活动”,决定开设以下体育活动项目:足球、乒乓球、篮球和羽毛球,要求每位学生必须且只能选择一项,为了解选择各种体育活动项目的学生人数,随机抽取了部分学生进行调查,并将通过调查获得的数据进行整理,绘制出以下两幅不完整的统计图,请根据统计图回答问题:
(1)这次活动一共调查了 名学生;
(2)补全条形统计图;
(3)在扇形统计图中,选择篮球项目的人数所在扇形的圆心角等于 度;
(4)若该学校有1500人,请你估计该学校选择足球项目的学生人数约是 人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=x2﹣2x+5与坐标轴的交点个数为( )
A.0个B.1个C.2个D.3个
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个袋中装有3个红球,5个黄球,3个白球,每个球除颜色外都相同,任意摸出一球, 摸到_____球的可能性最大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】x2﹣2x﹣15=0.
相关试题

