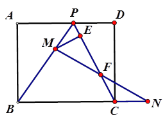
【题目】如图,在矩形ABCD中,AD=10,AB=8,点P在AD上,且BP=BC,点M在线段BP上,点N在线段BC的延长线上,且MP=NC,连接MN交线段PC于点F,过点M作ME⊥PC于点E,则EF= _______.
参考答案:
【答案】![]()
【解析】
过点M作MH∥BC交CP于H,根据两直线平行,同位角相等可得∠MHP=∠BCP,两直线平行,内错角相等可得∠NCF=∠MHF,根据等边对等角可得∠BCP=∠BPC,然后求出∠BPC=∠MHP,根据等角对等边可得PM=MH,根据等腰三角形三线合一的性质可得PE=EH,利用“角边角”证明△NCF和△MHF全等,根据全等三角形对应边相等可得CF=FH,从而求出EF=![]() CP,根据矩形的对边相等可得BC=AD=10,再利用勾股定理列式求出AP,然后求出PD,再次利用勾股定理列式计算即可求出CP,从而得解.
CP,根据矩形的对边相等可得BC=AD=10,再利用勾股定理列式求出AP,然后求出PD,再次利用勾股定理列式计算即可求出CP,从而得解.
如图,过点M作MH∥BC交CP于H,
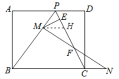
则∠MHP=∠BCP,∠NCF=∠MHF,
∵BP=BC,
∴∠BCP=∠BPC,
∴∠BPC=∠MHP,
∴PM=MH,
∵PM=CN,
∴CN=MH,
∵ME⊥CP,
∴PE=EH,
在△NCF和△MHF中,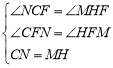 ,
,
∴△NCF≌△MHF(AAS),
∴CF=FH,
∴EF=EH+FH=![]() CP,
CP,
∵矩形ABCD中,AD=10,
∴BC=AD=10,
∴BP=BC=10,
在Rt△ABP中,AP=![]() =
=![]() =6,
=6,
∴PD=ADAP=106=4,
在Rt△CPD中,CP=![]() =
=![]() =
=![]() ,
,
∴EF=![]() CP=
CP=![]() ×
×![]() =
=![]() .
.
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
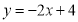 与
与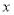 轴相交于点A,与
轴相交于点A,与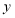 轴相交于点B.
轴相交于点B.(1)求A、B两点的坐标;
(2)求△AOB的面积;
(3)若点P是
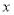 轴上的一个动点,且△PAB是等腰三角形,则P点的坐标为___________.
轴上的一个动点,且△PAB是等腰三角形,则P点的坐标为___________.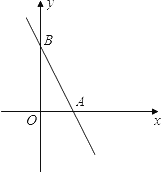
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
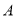 的坐标为
的坐标为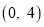 ,点
,点 的坐标为
的坐标为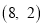 ,点
,点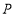 是
是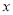 轴上一点,且
轴上一点,且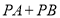 的值最小,
的值最小,(1)确定点
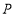 的位置,并求点
的位置,并求点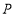 的坐标;
的坐标;(2)求
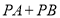 的最小值.
的最小值.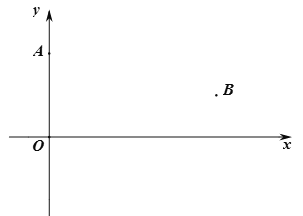
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,点E,F分别在BC,AD上,且BE:EC=2:1,EF∥CD,交对角线AC于点G,则
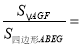 _____________。
_____________。
-
科目: 来源: 题型:
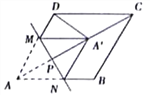
查看答案和解析>>【题目】菱形ABCD的边长是4,∠DAB=60,点M,N分别在边AD,AB上,MN⊥AC,垂足为P,把△AMN沿MN折叠得到△A'MN,若△A'DC恰为等腰三角形,则AP的长为_____。
-
科目: 来源: 题型:
查看答案和解析>>【题目】[材料阅读]
材料一:如图,
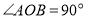 ,点
,点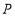 在
在 的平分线
的平分线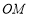 上,
上,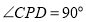 ,点
,点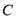 ,D分别在
,D分别在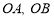 上.可求得如下结论:
上.可求得如下结论: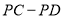 ,
,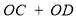 为定值.
为定值.材料二(性质):四边形的内角和为
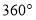 .
.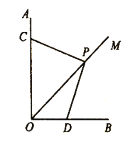
[问题解决]
(1)如图,点
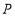 在
在 的平分线
的平分线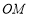 上,
上,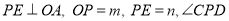 的边与
的边与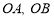 交于点
交于点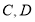 ,且
,且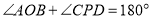 ,求
,求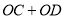 的值(用含
的值(用含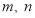 的式子表示).
的式子表示).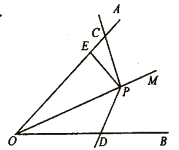
(2)如图,在平面直角坐标系中,直线
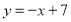 与
与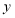 轴,
轴,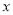 轴分别交于
轴分别交于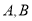 两点,点
两点,点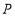 是
是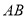 的中点,
的中点,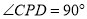 ,
,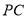 与
与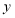 轴交于点
轴交于点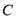 ,
,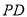 与
与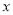 轴的正半轴交于点
轴的正半轴交于点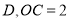 ,连接
,连接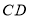 .求
.求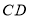 的长度.
的长度.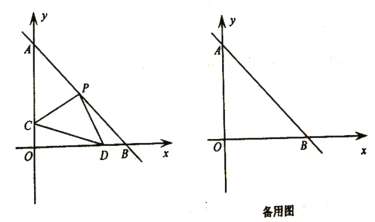
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年5月,某大型商业集团随机抽取所属的部分商业连锁店进行评估,将抽取的各商业连锁店按照评估成绩分成了
 、
、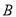 、
、 、
、 四个等级,并绘制了如下不完整的扇形统计图和条形统计图.
四个等级,并绘制了如下不完整的扇形统计图和条形统计图.根据以上信息,解答下列问题:
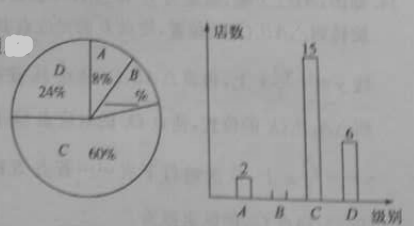
(1)本次评估随机抽取了多少家商业连锁店?
(2)请补充完整扇形统计图和条形统计图,并在图中标注相应数据;
(3)从
 、
、 两个等级的商业连锁店中任选2家介绍营销经验,求其中至少有一家是
两个等级的商业连锁店中任选2家介绍营销经验,求其中至少有一家是 等级的概率.
等级的概率.
相关试题

