【题目】如图,如图,抛物线y=x2+bx+c与x轴交于点A和点B(4,0),与y轴交于点C(0,4).
(1)求抛物线的解析式;
(2)若点M是抛物线在x轴下方的动点,过点M作MN∥y轴交直线BC于点N求线段MN的最大值;(3)在(2)的条件下,当MN取得最大值时,在抛物线的对称轴l上是否存在点P使△PBN是等腰三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由.

参考答案:
【答案】(1)y=x2-5x+4;(2)点p的坐标为(![]() ,
,![]() )、(
)、(![]() ,
,![]() ),(
),(![]() -
-![]() )、(
)、(![]() ,2+
,2+![]() ),或(
),或(![]() ,2-
,2-![]() ).
).
【解析】试题分析:
(1)把点B、C的坐标代入![]() 列出方程组,解方程组求得
列出方程组,解方程组求得![]() 的值即可得到二次函数的解析式;
的值即可得到二次函数的解析式;
(2)由点B、C的坐标可求出直线BC的解析式,设点M的横坐标为m,由此可用含m的代数式表示出点M、N的纵坐标,从而可用含m的式子表达出MN的长度,由点M在![]() 轴下方可求得m的取值范围为:
轴下方可求得m的取值范围为: ![]() ,由此即可求出线段MN的最大值;
,由此即可求出线段MN的最大值;
(3)由题意结合(2)可得点N的坐标,由点P在抛物线对称轴上,可设其坐标为(2.5,n),结合点B和点N的坐标即可表达出PB、PN、BN的长度,再分PB=PN、PB=BN、PN=BN三种情况讨论计算即可求得符合题意的点P的坐标.
试题解析:
(1)将点B(4,0)、C(0,4)代入抛物线y=x2+bx+c中,
得![]() ,得
,得![]() ,
,
∴抛物线的解析式为y=x2-5x+4.
(2)由题意可设点M的坐标为(m,m2-5m+4),设直线BC的解析式为y=kx+4,
把点(4,0)代入y=kx+4,中,
得:0=4k+4,解得:k=-1,
∴直线BC的解析式为y=-x+4.
∵MN∥y轴,
∴点N的坐标为(m,-m+4),
∴MN==-m+4-(m2-5m+4)=-(m-2)2+4.
∵抛物线的解析式为:y=x2-5x+4=(x-2.5)2,
∴抛物线的对称轴为x=2.5,
∴由点B的坐标为(4,0)可得点A的坐标为(1,0),
又∵点M在x轴下方,
∴1<m<4.
∴当m=2时,MN最大=4.
(3)由(2)可得:当m=2时,点N的坐标为(2,2),
∵点P在抛物线的对称轴上,
∴可设点P坐标为(2.5,n),
∴PB=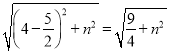 ,PN=
,PN= =
=![]() ,
,
BN=![]() =2
=2![]() ,
,
若![]() 为等腰三角形,则存在以下三种情况:
为等腰三角形,则存在以下三种情况:
①当![]() 时,即
时,即![]()
![]()
解得: ![]() ,此时点
,此时点![]() 的坐标为(
的坐标为(![]() ,
, ![]() );
);
②当![]() 时,即
时,即![]() =2
=2![]() ,解得:
,解得: ![]() ,
,
此时点![]() 的坐标为(
的坐标为(![]() ,
, ![]() )或(
)或(![]() ,
, ![]() );
);
③当![]() 时,即
时,即![]() =2
=2![]() ,解得:
,解得: ![]() ,
,
此时点![]() 的坐标为(
的坐标为(![]() ,2+
,2+![]() )或(
)或(![]() ,2
,2![]() ).
).
综上可知:在抛物线的对称轴![]() 上存在点
上存在点![]() ,使
,使![]() 是等腰三角形,点P的坐标为(
是等腰三角形,点P的坐标为(![]() ,
,![]() )、(
)、(![]() ,
,![]() ),(
),(![]() -
-![]() )、(
)、(![]() ,2+
,2+![]() ),或(
),或(![]() ,2-
,2-![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】郴州市正在创建“全国文明城市”,某校拟举办“创文知识”抢答赛,欲购买A、B两种奖品以鼓励抢答者.如果购买A种20件,B种15件,共需380元;如果购买A种15件,B种10件,共需280元.
(1)A、B两种奖品每件各多少元?
(2)现要购买A、B两种奖品共100件,总费用不超过900元,那么A种奖品最多购买多少件?
-
科目: 来源: 题型:
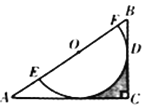
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,O为AB边上一点,⊙O交AB于点E,F两点,BC切⊙O于点D,且CD=
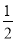 EF=1,
EF=1,(1)求证:AC与⊙O相切;
(2)求图中阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某课外小组的同学们在社会实践活动中调查了20户家庭莱月的用电量,如表所示则这20户家庭该月用电量的众数和中位数、平均数分别是( )

A. 180,160,164B. 160,180;164C. 160,160,164D. 180,180,164
-
科目: 来源: 题型:
查看答案和解析>>【题目】一项工程,甲,乙两公司合做,12天可以完成,共需付施工费102000元;如果甲,乙两公司单独完成此项工程,乙公司所用时间是甲公司的1.5倍,乙公司每天的施工费比甲公司每天的施工费少1500元.
(1)甲,乙两公司单独完成此项工程,各需多少天?
(2)若让一个公司单独完成这项工程,哪个公司的施工费较少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C为线段AB上一点,分别以AC,BC为边在AB的同侧作等边△HAC与等边△DCB,连接DH.
(1)如图1,当∠DHC=90°时,求
 的值;
的值;(2)在(1)的条件下,作点C关于直线DH的对称点E,连接AE,BE.求证:CE平分∠AEB.
(3)现将图1中的△DCB绕点C顺时针旋转一定角度α(0°<α<90°),如图2,点C关于直线DH的对称点为E,则(2)中的结论是否还成立,并证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校举行研学旅行活动,车上准备了7箱矿泉水,每箱的瓶数相同,到达目的地后,先从车上搬下3箱,发给每位同学1瓶矿泉水,有9位同学未领到.接着又从车上搬下4箱,继续分发,最后每位同学都有2瓶矿泉水,还剩下6瓶.问:有多少人参加此次研学旅行活动?每箱矿泉水有多少瓶?
相关试题

