Question

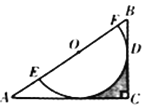
【题目】如图，在Rt△ABC中，∠C=90°，O为AB边上一点，⊙O交AB于点E，F两点，BC切⊙O于点D，且CD=EF=1，

（1）求证：AC与⊙O相切；

（2）求图中阴影部分的面积.

Answer 1

【答案】（1）见解析；（2）1﹣π．

【解析】试题分析：

（1）连接OD，过点O作OH⊥AC于点H，易证四边形ODCH是矩形，由此可得OH=CD=EF=OE，从而可得AC是⊙O的切线；

（2）由（1）可知∠DOH=90°，OH=EF=1，由此根据：S阴影=S正方形ODCH-S扇形ODH即可计算出阴影部分的面积.

试题解析：

（1）连接OD，过点O作OH⊥AC于点H，

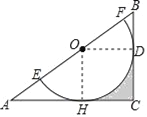
∵BC是⊙O的切线，

∴OD⊥BC．

∵∠C=90°，

∴∠OHC=∠ODC=∠C=90°，

∴四边形OHCD是矩形．

∵CD=EF，

∴OH=EF=OE．

∵OH⊥AC，

∴AC是⊙O的切线；

（2）由（1）可知，四边形ODCH是正方形，

∴∠DOH=90°，OH=CD=EF=1，

∴S阴影=S正方形ODCH-S扇形ODH=1×1﹣=1﹣π．