【题目】如图1,已知抛物线y=ax2+bx (a≠0)经过A(3,0)、B(4,4)两点.
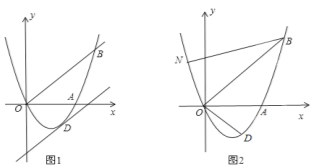
(1)求抛物线的解析式;
(2)将直线OB向下平移m个单位长度后,得到的直线与抛物线只有一个公共点D,求m的值及点D的坐标;
(3)如图2,若异于点A的点N在抛物线上,且∠NBO=∠ABO,求点N的坐标;
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() 点的坐标为
点的坐标为![]() ;(3)
;(3)![]()
【解析】
试题分析:(1)利用待定系数法求二次函数解析式进而得出答案即可;
根据已知条件可求出的解析式为![]() ,则向下平移
,则向下平移![]() 个单位长度后的解析式为:
个单位长度后的解析式为:![]() 由于抛物线与直线只有一个公共点,则联立解析式后得到的一元二次方程,其根的判别式等于0,由此可求出的值和点坐标;
由于抛物线与直线只有一个公共点,则联立解析式后得到的一元二次方程,其根的判别式等于0,由此可求出的值和点坐标;
设点![]() ,又点
,又点![]() 在抛物线
在抛物线![]() 上,代入抛物线的解析式即可求出
上,代入抛物线的解析式即可求出![]() 的值,进而得到
的值,进而得到![]() 的坐标.
的坐标.
试题解析:(1)抛物线![]() 经过
经过![]() ,将
,将![]() 与两点坐标代入得:
与两点坐标代入得:![]() ,解得:
,解得:![]() ,抛物线的解析式是
,抛物线的解析式是![]()
设直线![]() 的解析式为
的解析式为![]() ,由点
,由点![]() ,得:
,得:![]() ,解得:
,解得:![]() .直线
.直线![]() 的解析式为
的解析式为![]() ,直线
,直线![]() 向下平移
向下平移![]() 个单位长度后的解析式:
个单位长度后的解析式:![]()
![]() 在抛物线上,可设
在抛物线上,可设![]() 点D在直线
点D在直线![]() 上,
上,![]() ,即
,即![]() ,
,![]() 抛物线与直线只有一个公共点,
抛物线与直线只有一个公共点,![]() 解得:
解得:![]() 此时
此时![]()
![]()
![]() 点的坐标为
点的坐标为![]()
直线![]() 的解析式为
的解析式为![]() ,且A(3,0),
,且A(3,0),![]() 点A关于直线
点A关于直线![]() 的对称点
的对称点![]() 的坐标是(0,3),根据轴对称性质和三线合一性质得出
的坐标是(0,3),根据轴对称性质和三线合一性质得出![]() ,设直线
,设直线![]() 的解析式为
的解析式为![]() ,过点(4,4),
,过点(4,4),![]() 解得:
解得:![]() ,直线
,直线![]() 的解析式是
的解析式是![]() ,
,![]()
![]() 和
和![]() 重合,即点N在直线
重合,即点N在直线![]() 上,设点
上,设点![]() ,又点
,又点![]() 在抛物线
在抛物线![]() 上,
上,![]() 解得:
解得:![]() (不合题意,舍),
(不合题意,舍),![]()
-
科目: 来源: 题型:
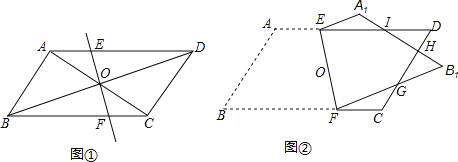
查看答案和解析>>【题目】(1)如图①,ABCD的对角线AC,BD交于点O,直线EF过点O,分别交AD,BC于点E,F.求证:AE=CF.
(2)如图②,将ABCD(纸片)沿过对角线交点O的直线EF折叠,点A落在点A1处,点B落在点B1处,设FB1交CD于点G,A1B1分别交CD,DE于点H,I.求证:EI=FG.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:二次函数y=﹣x2+bx+c的图象过点(﹣1,﹣8),(0,﹣3).
(1)求此二次函数的表达式,并用配方法将其化为y=a(x﹣h)2+k的形式;
(2)画出此函数图象的示意图.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个角的两边分别与另一个角的两边平行,若其中一个角为40°,则另一个角为_____________°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知正方形ABCD边长为1,点P是AD边上的一个动点,点A关于直线BP的对称点是点Q,连结PQ、DQ、CQ、BQ.设AP﹦x.
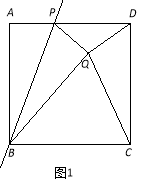

(1)BQ+DQ的最小值是 ,此时x的值是 ;
(2)如图2,若PQ的延长线交CD边于E,并且∠CQD=90°.
① 求证:QE﹦EC; ② 求x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:△ABC≌△DCB,若BC=10cm,AB=5cm,AC=7cm,则CD为( )
A. 10cm B. 7cm C. 5cm D. 5cm或7cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各条件中,不能作出唯一三角形的是( )
A. 已知两边和夹角 B. 已知两角和夹边
C. 已知两边和其中一边的对角 D. 已知三边
相关试题

