Question

【题目】九年级七班“数学兴趣小组”对函数的对称变换进行探究，以下是探究发现运用过程，请补充完整．
（1）操作发现，在作函数y=|x|的图象时，采用了分段函数的办法，该函数转化为y= ，请在如图1所示的平面直角坐标系中作出函数的图象；

（2）类比探究
作函数y=|x﹣1|的图象，可以转化为分段函数 ， 然后分别作出两段函数的图象．聪明的小昕，利用坐标平面上的轴对称知识，把函数y=x﹣1在x轴下面部分，沿x轴进行翻折，与x轴上及上面部分组成了函数y=|x﹣1|的图象，如图所示；

（3）拓展提高
如图2右图是函数y=x2﹣2x﹣3的图象，请在原坐标系作函数y=|x2﹣2x﹣3|的图象；

（4）实际运用
①函数 的图象与x轴有个交点，对应方程|x2﹣2x﹣3|=0有个实根；
②函数 的图象与直线y=5有个交点，对应方程|x2﹣2x﹣3|=5有个实根；
③函数 的图象与直线y=4有个交点，对应方程 有个实根；
④关于x的方程 有4个实根时，a的取值范围是 ．

Answer 1

【答案】
（1）

解：如图1，

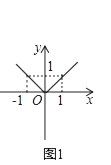
（2）
（3）

解：把函数y=x2﹣2x﹣3的图象在x轴下面部分，沿x轴进行翻折，与x轴上及上面部分组成了函数y=|x2﹣2x﹣3|的图象，如图2；

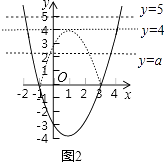
（4）2；2；2；2；3；3；0＜a＜4
【解析】解：（2.）类比探究
作函数y=|x﹣1|的图象，可以转化为分段函数y= ；（4）实际运用①函数y=|x2﹣2x﹣3|的图象与x轴有 2个交点，对应方程|x2﹣2x﹣3|=0有2个实根；②函数y=|x2﹣2x﹣3|的图象与直线y=5有 2个交点，对应方程|x2﹣2x﹣3|=5有2个实根；③函数y=|x2﹣2x﹣3|的图象与直线y=4有3个交点，对应方程|x2﹣2x﹣3|=4有3个实根；④关于x的方程|x2﹣2x﹣3|=a有4个实根时，a的取值范围是 0＜a＜4．
故答案为y= ；2，2；2，2；3，3；0＜a＜4．
（1）利用描点法画y=|x|的图象；（2）根据绝对值的意义，利用分类讨论的思想写出分段函数；（3）与（2）画函数图象的方法一样，把函数y=x2﹣2x﹣3的图象在x轴下面部分，沿x轴进行翻折可得到函数y=|x2﹣2x﹣3|的图象；（4）利用画函数图象，通过确定y=|x2﹣2x﹣3|的图象与直线y=a的交点个数解决问题．