【题目】用适当的方法解下面的方程
①3x2+x﹣1=0
②(3x﹣2)2=4(3﹣x)2 .
参考答案:
【答案】解:①3x2+x﹣1=0
a=3,b=1,c=﹣1,
△=b2﹣4ac=1+12=13>0,
x= ![]() ,
,
∴x1= ![]() ,x2=
,x2= ![]() .
.
②(3x﹣2)2=4(3﹣x)2 ,
移项得:(3x﹣2)2﹣4(3﹣x)2 , =0,
分解因式得:[(3x﹣2)+2(3﹣x)][(3x﹣2)﹣2(3﹣x)]=0,
可得x+4=0或5x﹣8=0,
解得:x1=﹣4,x2= ![]() .
.
【解析】①求出b2﹣4ac的值,再代入公式求出即可.②方程移项后利用因式分解法求出解即可.
【考点精析】根据题目的已知条件,利用公式法和因式分解法的相关知识可以得到问题的答案,需要掌握要用公式解方程,首先化成一般式.调整系数随其后,使其成为最简比.确定参数abc,计算方程判别式.判别式值与零比,有无实根便得知.有实根可套公式,没有实根要告之;已知未知先分离,因式分解是其次.调整系数等互反,和差积套恒等式.完全平方等常数,间接配方显优势.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在⊙O中,AB是弦,半径OC⊥AB,垂足为点D,要使四边形OACB为菱形,还需要添加一个条件,这个条件可以是( )
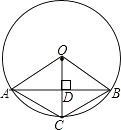
A.AD=BD
B.OD=CD
C.∠CAD=∠CBD
D.∠OCA=∠OCB -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为x=
 ,且经过点(2,0),有下列说法:①abc<0;②a+b=0;③4a+2b+c<0;④若(0,y1),(1,y2)是抛物线上的两点,则y1=y2 . 上述说法正确的是( )
,且经过点(2,0),有下列说法:①abc<0;②a+b=0;③4a+2b+c<0;④若(0,y1),(1,y2)是抛物线上的两点,则y1=y2 . 上述说法正确的是( ) 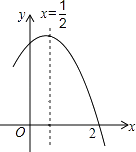
A.①②④
B.③④
C.①③④
D.①② -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=5cm,BC=12cm,将△ABC绕点B顺时针旋转60°,得到△BDE,连接DC交AB于点F,则△ACF与△BDF的周长之和为cm.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在日常生活中,观察各种建筑物的地板,就能发现地板常用各种正多边形地砖铺砌成美丽的图案.也就是说,使用给定的某些正多边形,能够拼成一个平面图形,既不留下一丝空白,又不互相重叠(在几何里叫做平面镶嵌).这显然与正多边形的内角大小有关.当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个周角(360°)时,就拼成了一个平面图形.
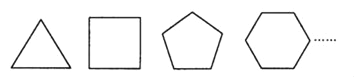
(1)请根据下列图形,填写表中空格:
正多边形边数
3
4
5
6
…
正多边形每个内角的度数
…
(2)如图,如果限于用一种正多边形镶嵌,哪几种正多边形能镶嵌成一个平面图形;
(3)正三角形、正四边形、正六边形中选一种,再在其他正多边形中选一种,请画出用这两种不同的正多边形镶嵌成的一个平面图形(草图);并探索这两种正多边形共能镶嵌成几种不同的平面图形?说明你的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
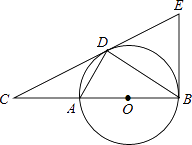
(1)判断直线CD和⊙O的位置关系,并说明理由.
(2)过点B作⊙O的切线BE交直线CD于点E,若AC=2,⊙O的半径是3,求BE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】九年级数学兴趣小组经过市场调查,得到某种运动服每月的销量与售价的相关信息如下表:
售价(元/件)
100
110
120
130
…
月销量(件)
200
180
160
140
…
已知该运动服的进价为每件60元,设售价为x元.
(1)请用含x的式子表示:①销售该运动服每件的利润是 ()元;②月销量是 ()件;(直接写出结果)
(2)设销售该运动服的月利润为y元,那么售价为多少时,当月的利润最大,最大利润是多少?
相关试题

