【题目】在日常生活中,观察各种建筑物的地板,就能发现地板常用各种正多边形地砖铺砌成美丽的图案.也就是说,使用给定的某些正多边形,能够拼成一个平面图形,既不留下一丝空白,又不互相重叠(在几何里叫做平面镶嵌).这显然与正多边形的内角大小有关.当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个周角(360°)时,就拼成了一个平面图形.
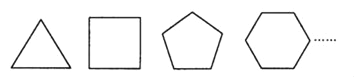
(1)请根据下列图形,填写表中空格:
正多边形边数 | 3 | 4 | 5 | 6 | … |
正多边形每个内角的度数 | … |
(2)如图,如果限于用一种正多边形镶嵌,哪几种正多边形能镶嵌成一个平面图形;
(3)正三角形、正四边形、正六边形中选一种,再在其他正多边形中选一种,请画出用这两种不同的正多边形镶嵌成的一个平面图形(草图);并探索这两种正多边形共能镶嵌成几种不同的平面图形?说明你的理由.
参考答案:
【答案】(1)见解析;(2)正三角形、正四边形(或正方形)、正六边形;(3)符合条件的图形只有一种.
【解析】
本题主要考查了平面镶嵌(密铺).(1)利用正多边形一个内角="180-"![]() 求解;
求解;
(2)进行平面镶嵌就是在同一顶点处的几个多边形的内角和应为360°,因此我们只需验证360°是不是上面所给的几个正多边形的一个内角度数的整数倍;
(3)常见的两种正多边形的密铺组合有:正三角形和正四边形能密铺,正六边形只能和正三角形密铺.所以要从正三角形、正四边形、正六边形中选一种,只能选择正四边形.
解:(1)由正n边形的内角的性质可分别求得正三角形、正方形、正五边形、正六边形、…、正n边形的每一个内角为:
60°,90°,108°,120°,…![]() ;
;
(2)如限于用一种正多边形镶嵌,则由一顶点的周围角的和等于360°得正三角形、正四边形(或正方形)、正六边形都能镶嵌成一个平面图形;
(3)如:正方形和正八边形(如图),
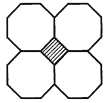
设在一个顶点周围有m个正方形的角,n个正八边形的角,
那么m,n应是方程m90°+n135°=360°的正整数解.
即2m+3n=8的正整数解,只有m=1,n=2一组,
∴符合条件的图形只有一种.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为x=
 ,且经过点(2,0),有下列说法:①abc<0;②a+b=0;③4a+2b+c<0;④若(0,y1),(1,y2)是抛物线上的两点,则y1=y2 . 上述说法正确的是( )
,且经过点(2,0),有下列说法:①abc<0;②a+b=0;③4a+2b+c<0;④若(0,y1),(1,y2)是抛物线上的两点,则y1=y2 . 上述说法正确的是( ) 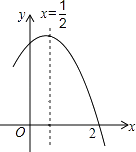
A.①②④
B.③④
C.①③④
D.①② -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=5cm,BC=12cm,将△ABC绕点B顺时针旋转60°,得到△BDE,连接DC交AB于点F,则△ACF与△BDF的周长之和为cm.

-
科目: 来源: 题型:
查看答案和解析>>【题目】用适当的方法解下面的方程
①3x2+x﹣1=0
②(3x﹣2)2=4(3﹣x)2 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
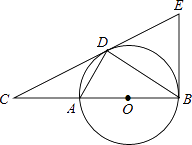
(1)判断直线CD和⊙O的位置关系,并说明理由.
(2)过点B作⊙O的切线BE交直线CD于点E,若AC=2,⊙O的半径是3,求BE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】九年级数学兴趣小组经过市场调查,得到某种运动服每月的销量与售价的相关信息如下表:
售价(元/件)
100
110
120
130
…
月销量(件)
200
180
160
140
…
已知该运动服的进价为每件60元,设售价为x元.
(1)请用含x的式子表示:①销售该运动服每件的利润是 ()元;②月销量是 ()件;(直接写出结果)
(2)设销售该运动服的月利润为y元,那么售价为多少时,当月的利润最大,最大利润是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】探究:如图1和2,四边形ABCD中,已知AB=AD,∠BAD=90°,点E、F分别在BC、CD上,∠EAF=45°.
(1)①如图1,若∠B、∠ADC都是直角,把△ABE绕点A逆时针旋转90°至△ADG,使AB与AD重合,则能证得
EF=BE+DF,请写出推理过程;
②如图2,若∠B、∠D都不是直角,则当∠B与∠D满足数量关系时,仍有EF=BE+DF;
(2)拓展:如图3,在△ABC中,∠BAC=90°,AB=AC=2 ,点D、E均在边BC上,且∠DAE=45°.若BD=1,求DE的长.
,点D、E均在边BC上,且∠DAE=45°.若BD=1,求DE的长.
相关试题

