【题目】如图,已知在⊙O中,AB是弦,半径OC⊥AB,垂足为点D,要使四边形OACB为菱形,还需要添加一个条件,这个条件可以是( ) 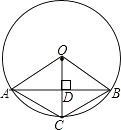
A.AD=BD
B.OD=CD
C.∠CAD=∠CBD
D.∠OCA=∠OCB
参考答案:
【答案】B
【解析】解:∵在⊙O中,AB是弦,半径OC⊥AB, ∴AD=DB,
当DO=CD,
则AD=BD,DO=CD,AB⊥CO,
故四边形OACB为菱形.
故选:B.
【考点精析】通过灵活运用菱形的判定方法和垂径定理,掌握任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形;垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将⊙O沿弦AB折叠,圆弧恰好经过圆心O,点P是优弧
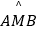 上一点,则∠APB的度数为( )
上一点,则∠APB的度数为( ) 
A.45°
B.30°
C.75°
D.60° -
科目: 来源: 题型:
查看答案和解析>>【题目】在同一坐标系中,一次函数y=ax+2与二次函数y=x2+a的图象可能是( )
A.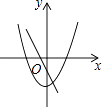
B.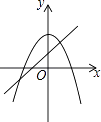
C.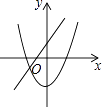
D.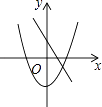
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们将在直角坐标系中圆心坐标和半径均为整数的圆称为“整圆”.如图,直线l:y=kx+4
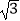 与x轴、y轴分别交于A、B,∠OAB=30°,点P在x轴上,⊙P与l相切,当P在线段OA上运动时,使得⊙P成为整圆的点P个数是( )
与x轴、y轴分别交于A、B,∠OAB=30°,点P在x轴上,⊙P与l相切,当P在线段OA上运动时,使得⊙P成为整圆的点P个数是( ) 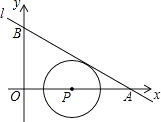
A.6
B.8
C.10
D.12 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为x=
 ,且经过点(2,0),有下列说法:①abc<0;②a+b=0;③4a+2b+c<0;④若(0,y1),(1,y2)是抛物线上的两点,则y1=y2 . 上述说法正确的是( )
,且经过点(2,0),有下列说法:①abc<0;②a+b=0;③4a+2b+c<0;④若(0,y1),(1,y2)是抛物线上的两点,则y1=y2 . 上述说法正确的是( ) 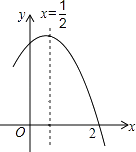
A.①②④
B.③④
C.①③④
D.①② -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=5cm,BC=12cm,将△ABC绕点B顺时针旋转60°,得到△BDE,连接DC交AB于点F,则△ACF与△BDF的周长之和为cm.

-
科目: 来源: 题型:
查看答案和解析>>【题目】用适当的方法解下面的方程
①3x2+x﹣1=0
②(3x﹣2)2=4(3﹣x)2 .
相关试题

