【题目】在平面直角坐标系内,双曲线:y= ![]() (x>0)分别与直线OA:y=x和直线AB:y=﹣x+10,交于C,D两点,并且OC=3BD.
(x>0)分别与直线OA:y=x和直线AB:y=﹣x+10,交于C,D两点,并且OC=3BD. 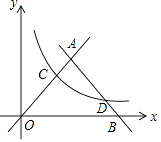
(1)求出双曲线的解析式;
(2)连结CD,求四边形OCDB的面积.
参考答案:
【答案】
(1)解:过点A、C、D作x轴的垂线,垂足分别是M、E、F,
∴∠AMO=∠CEO=∠DFB=90°,
∵直线OA:y=x和直线AB:y=﹣x+10,
∴∠AOB=∠ABO=45°,
∴△CEO∽△DEB
∴ ![]() =
= ![]() =3,
=3,
设D(10﹣m,m),其中m>0,
∴C(3m,3m),
∵点C、D在双曲线上,
∴9m2=m(10﹣m),
解得:m=1或m=0(舍去)
∴C(3,3),
∴k=9,
∴双曲线y= ![]() (x>0)
(x>0)
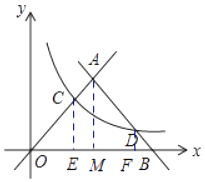
(2)解:由(1)可知D(9,1),C(3,3),B(10,0),
∴OE=3,EF=6,DF=1,BF=1,
∴S四边形OCDB=S△OCE+S梯形CDFE+S△DFB
= ![]() ×3×3+
×3×3+ ![]() ×(1+3)×6+
×(1+3)×6+ ![]() ×1×1=17,
×1×1=17,
∴四边形OCDB的面积是17
【解析】(1)过点A、C、D作x轴的垂线,垂足分别是M、E、F,由直线y=x和y=﹣x+10可知∠AOB=∠ABO=45°,证明△CEO∽△DEB,从而可知 ![]() =
= ![]() =3,然后设设D(10﹣m,m),其中m>0,从而可知C的坐标为(3m,3m),利用C、D在反比例函数图象上列出方程即可求出m的值.(2)求分别求出△OCE、△DFB△、梯形CDFE的面积即可求出答案.
=3,然后设设D(10﹣m,m),其中m>0,从而可知C的坐标为(3m,3m),利用C、D在反比例函数图象上列出方程即可求出m的值.(2)求分别求出△OCE、△DFB△、梯形CDFE的面积即可求出答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C在线段AB上,AC=8cm,CB=6cm,点M、N分别是AC、BC的中点.
(1)求线段MN的长;
(2)若C为线段AB上任一点,满足AC+CB=a cm,其它条件不变,你能猜想MN的长度吗?并说明理由;
(3)若C在线段AB的延长线上,且满足AC﹣BC=b cm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?并说明理由;

-
科目: 来源: 题型:
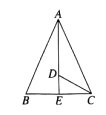
查看答案和解析>>【题目】如图,在△ABC中,已知AB=AC,∠BAC和∠ACB的平分线相交于点D,∠ADC=125°,求∠ACB和∠BAC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列代数式:
(1)
 ; (2)ab÷c2; (3)
; (2)ab÷c2; (3)  ; (4)
; (4) 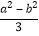 ; (5)2x(a+b); (6)ab·2.
; (5)2x(a+b); (6)ab·2.符合代数式书写要求的有几个?答:( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】一张长为a宽为b的铁板(a>b),从四个角截去四个边长为x的小正方形
 ,做成一个无盖的盒子,用代数式表示:
,做成一个无盖的盒子,用代数式表示:(1)无盖盒子的外表面积;(用两种方法)
(2)无盖盒子的容积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2016年12月底我国首艘航空母舰辽宁舰与数艘去驱航舰组成编队,携多架歼﹣15舰载战斗机和多型舰载直升机开展跨海区训练和试验任务,在某次演习中,预警直升机A发现在其北偏东60°,距离160千米处有一可疑目标B,预警直升机立即向位于南偏西30°距离40千米处的航母C报告,航母舰载战斗机立即升空沿北偏东53°方向向可疑目标飞去,请求出舰载战斗机到达目标的航程BC.
(结果保留整数,参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.3, ≈1.73)
≈1.73)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB,CD相交于点O,OE平分∠AOC,∠AOD比∠AOE大75°,求∠AOD的度数.

相关试题

