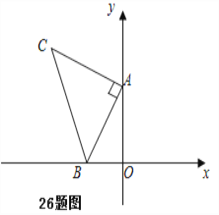
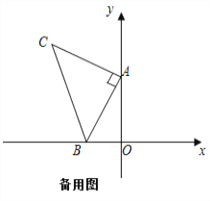
【题目】如图,平面直角坐标系中有点B(﹣1,0)和y轴上一动点A(0,a),其中a>0,以A点为直角顶点在第二象限内作等腰直角△ABC,设点C的坐标为(c,d).
(1)当a=2时,则C点的坐标为( , );
(2)动点A在运动的过程中,试判断c+d的值是否发生变化?若不变,请求出其值;若发生变化,请说明理由.
(3)当a=2时,在坐标平面内是否存在一点P(不与点C重合),使△PAB与△ABC全等?若存在,直接写出P点坐标;若不存在,请说明理由.
参考答案:
【答案】(1)C(-2,3);(2)c+d的值不变,c+d=1(3)P点坐标(-3,1)、(2,1)、(1,-1).
【解析】试题(1)先过点C作CE⊥y轴于E,证△AEC≌△BOA,推出CE=OA=2,AE=BO=1,即可得出点C的坐标;(2)、先过点C作CE⊥y轴于E,证△AEC≌△BOA,推出CE=OA=a,AE=BO=1,可得OE=a=1,即可得出点C的坐标为(-a,a+1),据此可得c+d的值不变;(3)、分为三种情况讨论,分别画出符合条件的图形,构造直角三角形,证出三角形全等,根据全等三角形对应边相等即可得出答案.
试题解析:(1)、C(-2,3);
(2)、 动点A在运动的过程中c+d的值不变.
过点C作CE⊥y轴于E,则∠CEA=∠AOB, ∵△ABC是等腰直角三角形,
∴AC=BA,∠BAC=90°,∴∠ACE+∠CAE=90°=∠BAO+∠CAE,∴∠ACE=∠BAO,
∴△ACE≌△BAO, ∵B(-1,0),A(0,a),∴BO=AE=1,AO=CE=a,
∴OE=a+1,∴C(-a,1+a), 又∵点C的坐标为(c,d),
∴c+d=-a+1+a=1,即c+d的值不变;
(3)、P点坐标(-3,1)、(2,1)、(1,-1).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,点D为射线CB上一个动点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,过点E作EF∥BC,交直线AC于点F,连接CE.
(1)如图①,若∠BAC=60°,按边分类:△CEF是 ____________ 三角形;
(2)若∠BAC<60°.
①如图②,当点D在线段CB上移动时,判断△CEF的形状并证明;
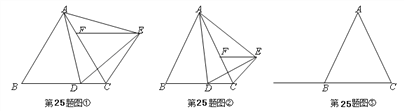
②当点D在线段CB的延长线上移动时,△CEF是什么三角形?请在图③中画出相应的图形,写出结论并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】丽水苛公司将“丽水山耕”农副产品运往杭州市场进行销售.记汽车行驶时间为t小时,平均速度为v千米/小时(汽车行驶速度不超过100千米/小时).根据经验,v,t的一组对应值如下表:
v(千米/小时)
75
80
85
90
95
t(小时)
4.00
3.75
3.53
3.33
3.16
(1)根据表中的数据,求出平均速度v(千米/小时)关于行驶时间t(小时)的函数表达式;
(2)汽车上午7:30从丽水出发,能否在上午10:00之前到达杭州市?请说明理由:
(3)若汽车到达杭州市场的行驶时间t满足3.5≤t≤4,求平均速度v的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】判断下列各式从等号左边到右边的变形,哪些是整式乘法,哪些是因式分解.
(1)a2-9b2=(a+3b)(a-3b);
(2)3y(x+2y)=3xy+6y2;
(3)(3a-1)2=9a2-6a+1;
(4)4y2+12y+9=(2y+3)2;
(5)x2+x=x2(1+
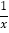 );
);(6)x2-y2+4y-4=(x-y)(x+y)+4(y-1).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知DE∥BC, AB∥CD,E为AB的中点,∠A=∠B.下列结论:①CD=AE;②AC=DE;③AC平分∠BCD;④O点是DE的中点;⑤AC=AB.其中正确的是( )
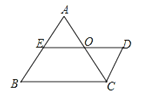
A. ①②④ B. ①③⑤ C. ②③④ D. ②④⑤
-
科目: 来源: 题型:
查看答案和解析>>【题目】将含有30°角的直角三角板OAB如图放置在平面直角坐标系中,OB在x轴上,若OA=2,将三角板绕原点O顺时针旋转75°,则点A的对应点A′的坐标为( )
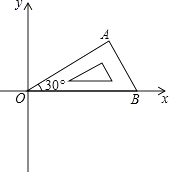
A.(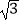 ,﹣1)
,﹣1)
B.(1,﹣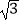 )
)
C.(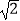 ,﹣
,﹣ 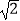 )
)
D.(﹣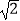 ,
, 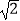 )
) -
科目: 来源: 题型:
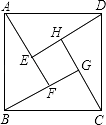
查看答案和解析>>【题目】如图是我国汉代数学家赵爽在注解《周脾算经》时给出的“赵爽弦图”,图中的四个直角三角形是全等的,如果大正方形ABCD的面积是小正方形EFGH面积的13倍,那么tan∠ADE的值为( )
A.
B.
C.
D.
相关试题

