【题目】如图所示,在平行四边形ABCD中,AD∥BC,过B作BE⊥AD交AD于点E,AB=13cm,BC=21cm,AE=5cm.动点P从点C出发,在线段CB上以每秒1cm的速度向点B运动,动点Q同时从点A出发,在线段AD上以每秒2cm的速度向点D运动,当其中一个动点到达端点时另一个动点也随之停止运动,设运动的时间为t(秒)
(1)当t为何值时,四边形PCDQ是平行四边形?
(2)当t为何值时,△QDP的面积为60cm2?
(3)当t为何值时,PD=PQ?

参考答案:
【答案】(1)当t=7时,四边形PCDQ是平行四边形;(2)当t=![]() 时,△QDP的面积为60cm2;(3)当t=
时,△QDP的面积为60cm2;(3)当t=![]() 时,PD=PQ.
时,PD=PQ.
【解析】
(1)根据题意用t表示出CP=t,AQ=2t,根据平行四边形的判定定理列出方程,解方程即可;
(2)根据三角形的面积公式列方程,解方程得到答案;
(3)根据等腰三角形的三线合一得到DH=![]() DQ,列方程计算即可.
DQ,列方程计算即可.
(1)由题意得,CP=t,AQ=2t,
∴QD=21﹣2t,
∵AD∥BC,
∴当DQ=PC时,四边形PCDQ是平行四边形,
则21﹣2t=t,
解得,t=7,
∴当t=7时,四边形PCDQ是平行四边形;
(2)在Rt△ABE中,BE=![]() =12,
=12,
由题意得,![]() ×(21﹣2t)×12=60,
×(21﹣2t)×12=60,
解得,t=![]() ,
,
∴当t=![]() 时,△QDP的面积为60cm2;
时,△QDP的面积为60cm2;
(3)作PH⊥DQ于H,DG⊥BC于G,则四边形HPGD为矩形,

∴PG=HD,
由题意得,CG=AE=5,
∴PG=t﹣5,
当PD=PQ,PH⊥DQ时,DH=![]() DQ,即t﹣5=
DQ,即t﹣5=![]() (21﹣2t),
(21﹣2t),
解得,t=![]() ,
,
则当t=![]() 时,PD=PQ.
时,PD=PQ.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,点D,E分别是边AB,AC的中点,连接DE、BE,点F,G,H分别为BE,DE,BC的中点.
(1)求证:FG=FH;
(2)若∠A=90°,求证:FG⊥FH;
(3)若∠A=80°,求∠GFH的度数.

-
科目: 来源: 题型:
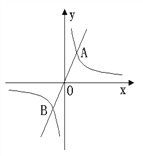
查看答案和解析>>【题目】如图,已知正比例函数y=kx的图象与反比例函数y=
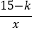 的图象相交于A、B两点,且A点的横坐标为2.
的图象相交于A、B两点,且A点的横坐标为2.(1)求A、B两点的坐标;
(2)在x轴上取关于原点对称的P、Q两点,(P点在Q点的右边),试问四边形AQBP一定是一个什么形状的四边形?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校九年级举行乒乓球比赛,准备发放一些奖品进行奖励,奖品设为一等奖和二等奖.已知购买一个一等奖奖品比购买一个二等奖奖品多用20元.若用400元购买一等奖奖品的个数是用160元购买二等奖奖品个数的一半.
(1)求购买一个一等奖奖品和一个二等奖奖品各需多少元?
(2)经商谈,商店决定给予该学校购买一个一等奖奖品即赠送一个二等奖奖品的优惠,如果该学校需要二等奖奖品的个数是一等奖奖品个数的2倍还多8个,且该学校购买两个奖项奖品的总费用不超过670元,那么该学校最多可购买多少个一等奖奖品?
-
科目: 来源: 题型:
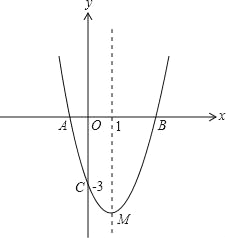
查看答案和解析>>【题目】(11分)如图,抛物线y=ax2+bx﹣3与x轴交于A,B两点,与y轴交于C点,且经过点(2,﹣3a),对称轴是直线x=1,顶点是M.
(1)求抛物线对应的函数表达式;
(2)经过C,M两点作直线与x轴交于点N,在抛物线上是否存在这样的点P,使以点P,A,C,N为顶点的四边形为平行四边形?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)设直线y=﹣x+3与y轴的交点是D,在线段BD上任取一点E(不与B,D重合),经过A,B,E三点的圆交直线BC于点F,试判断△AEF的形状,并说明理由;
(4)当E是直线y=﹣x+3上任意一点时,(3)中的结论是否成立(请直接写出结论).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂为了对新研发的一种产品进行合理定价,将该产品按拟定的价格进行试销,通过对5天的试销情况进行统计,得到如下数据:

(1)通过对上面表格中的数据进行分析,发现销量y(件)与单价
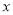 (元/件)之间存在一次函数关系,求y关于
(元/件)之间存在一次函数关系,求y关于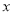 的函数关系式(不需要写出函数自变量的取值范围);
的函数关系式(不需要写出函数自变量的取值范围); (2)预计在今后的销售中,销量与单价仍然存在(2)中的关系,且该产品的成本是20元/件.为使工厂获得最大利润,该产品的单价应定为多少?
(3)为保证产品在实际试销中销售量不得低于30件,且工厂获得得利润不得低于400元,请直接写出单价
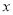 的取值范围;
的取值范围; -
科目: 来源: 题型:
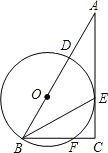
查看答案和解析>>【题目】在Rt△ABC中,∠ACB=90°,BE平分∠ABC,D是边AB上一点,以BD为直径的⊙O经过点E,且交BC于点F.
(1)求证:AC是⊙O的切线;
(2)若BF=6,⊙O的半径为5,求CE的长.
相关试题

