【题目】某工厂为了对新研发的一种产品进行合理定价,将该产品按拟定的价格进行试销,通过对5天的试销情况进行统计,得到如下数据:

(1)通过对上面表格中的数据进行分析,发现销量y(件)与单价![]() (元/件)之间存在一次函数关系,求y关于
(元/件)之间存在一次函数关系,求y关于![]() 的函数关系式(不需要写出函数自变量的取值范围);
的函数关系式(不需要写出函数自变量的取值范围);
(2)预计在今后的销售中,销量与单价仍然存在(2)中的关系,且该产品的成本是20元/件.为使工厂获得最大利润,该产品的单价应定为多少?
(3)为保证产品在实际试销中销售量不得低于30件,且工厂获得得利润不得低于400元,请直接写出单价![]() 的取值范围;
的取值范围;
参考答案:
【答案】(1)![]() ;(2)最大值为450元;(3)
;(2)最大值为450元;(3)![]()
【解析】试题分析:(1)设y=kx+b,根据表中数据,利用待定系数法求解可得;
(2)设工厂获得的利润为w元,根据:“总利润=每件利润×销售量”,列函数解析式并配方可得其最值情况;
(3)根据销售量≥30件、获得的利润≥400元列不等式组,解不等式组可得.
试题解析:(1)设y=kx+b,
将x=30、y=40,x=34、y=32,代入y=kx+b,
得: ![]() ,
,
解得: ![]() ,
,
∴y关于x的函数关系式为:y=-2x+100;
(2)设定价为x元时,工厂获得的利润为w元,
则w=(x-20)y=-2x2+140x-2000=-2(x-35)2+450
∴当x=35时,w的最大值为450元.
(3)根据题意得:
![]()
解得:30≤x≤35.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用锤子以相同的力将铁钉垂直钉入木块,随着铁钉的深入,铁钉所受的阻力也越来越大.当未进入木块的钉子长度足够时,每次钉入木块的钉子长度是前一次的
 .已知这个铁钉被敲击3次后全部进入木块(木块足够厚),且第一次敲击后铁钉进入木块的长度是2 cm,若铁钉总长度为a cm,则a满足( )
.已知这个铁钉被敲击3次后全部进入木块(木块足够厚),且第一次敲击后铁钉进入木块的长度是2 cm,若铁钉总长度为a cm,则a满足( )
A.2.5<a<4
B.2.5≤a<3.5
C.3≤a<4
D.3<a≤3.5 -
科目: 来源: 题型:
查看答案和解析>>【题目】若满足不等式20<5-2(2+2x)<50的最大整数解为a,最小整数解为b,则a+b之值为何?( )
A.-15
B.-16
C.-17
D.-18 -
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:(2x+1)(2x﹣1)﹣3x(x+1)﹣(x﹣1)2 , 当x=﹣1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线

(1)证明:不论m为何值,抛物线图象的顶点
 均在某一直线
均在某一直线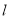 的图象上,求此直线
的图象上,求此直线 的函数解析式;
的函数解析式;(2)当
 时,点P为抛物线上一点,且
时,点P为抛物线上一点,且 ,求点P的坐标;
,求点P的坐标;(3)将(2)中的抛物线
 沿x轴翻折再向上平移1个单位向右平移
沿x轴翻折再向上平移1个单位向右平移 个单位得抛物线
个单位得抛物线 ,设抛物线
,设抛物线 的顶点为
的顶点为 ,抛物线
,抛物线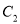 与
与 轴相交于点
轴相交于点 (A在B的左边),且
(A在B的左边),且 ∥
∥ ,求
,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】若-3x2my3与2x4yn是同类项,那么m-n=__________
-
科目: 来源: 题型:
查看答案和解析>>【题目】宁波轨道交通1号线、2号线建设总投资253.7亿元,其中253.7亿用科学记数法表示为( )
A.253.7×108
B.25.37×109
C.2.537×1010
D.2.537×1011
相关试题

