【题目】如图,已知射线CD∥OA,点E、点F是OA上的动点,CE平分∠OCF,且满足∠FCA=∠FAC.
(1)若∠O=∠ADC,判断AD与OB的位置关系,证明你的结论.
(2)若∠O=∠ADC=60°,求∠ACE的度数.
(3)在(2)的条件下左右平行移动AD,∠OEC和∠CAD存在怎样的数量关系?请直接写出结果(不需写证明过程)
参考答案:
【答案】
(1)解:∵CD∥OA,
∴∠BCD=∠O,
∵∠O=∠ADC,
∴∠BCD=∠CDA,
∴AD∥OB;
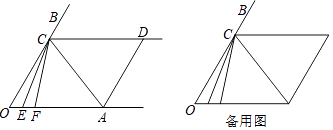
(2)解:∵∠O=∠ADC=60°,
∴∠BCD=60°,
∴∠OCD=120°,
∵CD∥OA,
∴∠DCA=∠CAO,
∵∠FCA=∠FAC,
∴∠DCA=FCA,
∵CE平分∠OCF,
∴∠OCE=∠FCE,
∴∠ECF+∠ACF= ![]() ∠OCD=60°,
∠OCD=60°,
∴∠ACE=60°;
(3)解:∠CAD+∠OEC=180°,
理由:∵AD∥OC,
∴∠CAD=∠OCA,
∵∠OCA=∠OCE+∠ACE=60°+∠OCE,
∵∠AEC=∠O+∠OCE=60°+∠OCE,
∴∠AEC=∠CAD,
∵∠AEC+∠OEC=180°,
∴∠CAD+∠OEC=180°.
【解析】(1)首先根据平行线的性质得到∠BCD=∠O,然后通过等量代换得到∠BCD=∠CDA,于是得到结论;
(2)首先依据邻补角的定义得到∠OCD=120°,然后再根据平行线的性质得到∠DCA=∠CAO,通过等量代换得到∠DCA=FCA,由角平分线的定义得到∠OCE=∠FCE,于是得到结论;
(3)首先根据平行线的性质得到∠CAD=∠OCA,然后可推出∠AEC=∠CAD,接下来,根据平角的定义得到∠AEC+∠OEC=180°,于是得到结论.
【考点精析】根据题目的已知条件,利用平行线的性质和平移的性质的相关知识可以得到问题的答案,需要掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;①经过平移之后的图形与原来的图形的对应线段平行(或在同一直线上)且相等,对应角相等,图形的形状与大小都没有发生变化;②经过平移后,对应点所连的线段平行(或在同一直线上)且相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1所示,已知抛物线
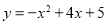 的顶点为D,与x轴交于A、B两点,与y轴交于C点,E为对称轴上的一点,连接CE,将线段CE绕点E按逆时针方向旋转90°后,点C的对应点C′恰好落在y轴上.
的顶点为D,与x轴交于A、B两点,与y轴交于C点,E为对称轴上的一点,连接CE,将线段CE绕点E按逆时针方向旋转90°后,点C的对应点C′恰好落在y轴上.(1)直接写出D点和E点的坐标;
(2)点F为直线C′E与已知抛物线的一个交点,点H是抛物线上C与F之间的一个动点,若过点H作直线HG与y轴平行,且与直线C′E交于点G,设点H的横坐标为m(0<m<4),那么当m为何值时,
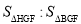 =5:6?
=5:6?(3)图2所示的抛物线是由
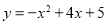 向右平移1个单位后得到的,点T(5,y)在抛物线上,点P是抛物线上O与T之间的任意一点,在线段OT上是否存在一点Q,使△PQT是等腰直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.
向右平移1个单位后得到的,点T(5,y)在抛物线上,点P是抛物线上O与T之间的任意一点,在线段OT上是否存在一点Q,使△PQT是等腰直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.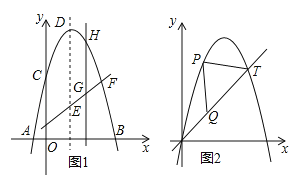
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线
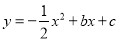 与坐标轴分别交于点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动.
与坐标轴分别交于点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动.(1)直接写出抛物线的解析式: ;
(2)求△CED的面积S与D点运动时间t的函数解析式;当t为何值时,△CED的面积最大?最大面积是多少?
(3)当△CED的面积最大时,在抛物线上是否存在点P(点E除外),使△PCD的面积等于△CED的最大面积?若存在,求出P点的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2017年我国约有9400000人参加高考,将9400000用科学记数法表示为 .
-
科目: 来源: 题型:
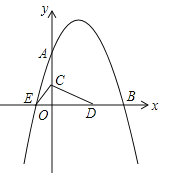
查看答案和解析>>【题目】如图,点P是∠AOB的边OB上的一点,过点P画OB的垂线,交OA于点C;

(1)①过点C画OB的平行线CD;②过点P画OA的垂线,垂足为H;
(2)线段PH的长度是点P到的距离,线段的长度是点C到直线OB的距离.线段PC、PH、OC这三条线段大小关系是(用“<”号连接). -
科目: 来源: 题型:
查看答案和解析>>【题目】某课题小组为了解某品牌电动自行车的销售情况,对某专卖店第一季度该品牌A、B、C、D四种型号电动车的销量做了统计,绘制成如图所示的两幅统计图(均不完整)
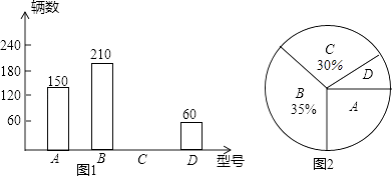
(1)该店第一季度售出这种品牌的电动自行车共多少辆?
(2)把两幅统计图补充完整. -
科目: 来源: 题型:
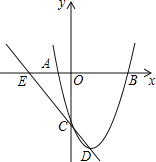
查看答案和解析>>【题目】如图,已知抛物线经过点A(﹣2,0)、B(4,0)、C(0,﹣8).
(1)求抛物线的解析式及其顶点D的坐标;
(2)直线CD交x轴于点E,过抛物线上在对称轴的右边的点P,作y轴的平行线交x轴于点F,交直线CD于M,使PM=
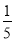 EF,请求出点P的坐标;
EF,请求出点P的坐标;(3)将抛物线沿对称轴平移,要使抛物线与(2)中的线段EM总有交点,那么抛物线向上最多平移多少个单位长度,向下最多平移多少个单位长度.
相关试题

