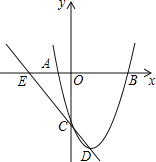
【题目】如图,已知抛物线经过点A(﹣2,0)、B(4,0)、C(0,﹣8).
(1)求抛物线的解析式及其顶点D的坐标;
(2)直线CD交x轴于点E,过抛物线上在对称轴的右边的点P,作y轴的平行线交x轴于点F,交直线CD于M,使PM=![]() EF,请求出点P的坐标;
EF,请求出点P的坐标;
(3)将抛物线沿对称轴平移,要使抛物线与(2)中的线段EM总有交点,那么抛物线向上最多平移多少个单位长度,向下最多平移多少个单位长度.
参考答案:
【答案】(1)![]() ,顶点D的坐标为(1,﹣9);(2)P(2,﹣8);(3)抛物线向上最多平移
,顶点D的坐标为(1,﹣9);(2)P(2,﹣8);(3)抛物线向上最多平移![]() 个单位长度,向下最多平移72个单位长度.
个单位长度,向下最多平移72个单位长度.
【解析】
试题分析:(1)由于抛物线与x轴的两个交点已知,抛物线的解析式可设成交点式:y=a(x+2)(x﹣4),然后将点C的坐标代入就可求出抛物线的解析式,再将该解析式配成顶点式,即可得到顶点坐标.
(2)先求出直线CD的解析式,再求出点E的坐标,然后设点P的坐标为(m,n),从而可以用m的代数式表示出PM、EF,然后根据PM=![]() EF建立方程,就可求出m,进而求出点P的坐标.
EF建立方程,就可求出m,进而求出点P的坐标.
(3)先求出点M的坐标,然后设平移后的抛物线的解析式为![]() ,然后只需考虑三个临界位置(①向上平移到与直线EM相切的位置,②向下平移到经过点M的位置,③向下平移到经过点E的位置)所对应的c的值,就可以解决问题.
,然后只需考虑三个临界位置(①向上平移到与直线EM相切的位置,②向下平移到经过点M的位置,③向下平移到经过点E的位置)所对应的c的值,就可以解决问题.
试题解析:(1)根据题意可设抛物线的解析式为y=a(x+2)(x﹣4).
∵点C(0,﹣8)在抛物线y=a(x+2)(x﹣4)上,∴﹣8a=﹣8,∴a=1,∴y=(x+2)(x﹣4)=![]() ,即
,即![]() ,∴抛物线的解析式为
,∴抛物线的解析式为![]() ,顶点D的坐标为(1,﹣9);
,顶点D的坐标为(1,﹣9);
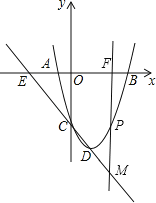
(2)如图,设直线CD的解析式为y=kx+b,∴![]() ,解得:
,解得:![]() ,∴直线CD的解析式为y=﹣x﹣8.当y=0时,﹣x﹣8=0,则有x=﹣8,∴点E的坐标为(﹣8,0).
,∴直线CD的解析式为y=﹣x﹣8.当y=0时,﹣x﹣8=0,则有x=﹣8,∴点E的坐标为(﹣8,0).
设点P的坐标为(m,n),则PM=![]() =
=![]() ,EF=m﹣(﹣8)=m+8.
,EF=m﹣(﹣8)=m+8.
∵PM=![]() EF,∴
EF,∴![]() .整理得:
.整理得:![]() ,∴(5m+4)(m﹣2)=0,解得:m=
,∴(5m+4)(m﹣2)=0,解得:m=![]() 或m=2.∵点P在对称轴x=1的右边,∴m=2.此时,n=
或m=2.∵点P在对称轴x=1的右边,∴m=2.此时,n=![]() ﹣2×2﹣8=﹣8,∴点P的坐标为(2,﹣8);
﹣2×2﹣8=﹣8,∴点P的坐标为(2,﹣8);
(3)当m=2时,y=﹣2﹣8=﹣10,∴点M的坐标为(2,﹣10).
设平移后的抛物线的解析式为![]() ,①若抛物线
,①若抛物线![]() 与直线y=﹣x﹣8相切,则方程
与直线y=﹣x﹣8相切,则方程![]() 即
即![]() 有两个相等的实数根,∴1﹣4×1×c=0,∴c=
有两个相等的实数根,∴1﹣4×1×c=0,∴c=![]() ;
;
②若抛物线![]() 经过点M,则有
经过点M,则有![]() ,∴c=﹣2;
,∴c=﹣2;
③若抛物线![]() 经过点E,则有
经过点E,则有![]() ,∴c=﹣72.
,∴c=﹣72.
综上所述:要使抛物线与(2)中的线段EM总有交点,抛物线向上最多平移![]() 个单位长度,向下最多平移72个单位长度.
个单位长度,向下最多平移72个单位长度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知射线CD∥OA,点E、点F是OA上的动点,CE平分∠OCF,且满足∠FCA=∠FAC.

(1)若∠O=∠ADC,判断AD与OB的位置关系,证明你的结论.
(2)若∠O=∠ADC=60°,求∠ACE的度数.
(3)在(2)的条件下左右平行移动AD,∠OEC和∠CAD存在怎样的数量关系?请直接写出结果(不需写证明过程) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P是∠AOB的边OB上的一点,过点P画OB的垂线,交OA于点C;

(1)①过点C画OB的平行线CD;②过点P画OA的垂线,垂足为H;
(2)线段PH的长度是点P到的距离,线段的长度是点C到直线OB的距离.线段PC、PH、OC这三条线段大小关系是(用“<”号连接). -
科目: 来源: 题型:
查看答案和解析>>【题目】某课题小组为了解某品牌电动自行车的销售情况,对某专卖店第一季度该品牌A、B、C、D四种型号电动车的销量做了统计,绘制成如图所示的两幅统计图(均不完整)
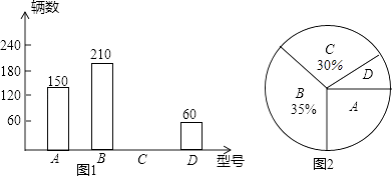
(1)该店第一季度售出这种品牌的电动自行车共多少辆?
(2)把两幅统计图补充完整. -
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=ax2﹣2x与x轴正半轴相交于点A,顶点为B.
(1)用含a的式子表示点B的坐标;
(2)经过点C(0,﹣2)的直线AC与OB(O为原点)相交于点D,与抛物线的对称轴相交于点E,△OCD≌△BED,求a的值.
-
科目: 来源: 题型:
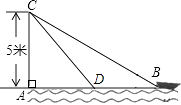
查看答案和解析>>【题目】如图,在离水面高度为5米的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为13米,此人以0.5米每秒的速度收绳,10秒后船移动到点D的位置,问船向岸边移动了多少米?(假设绳子是直的,结果保留根号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】“丹棱冻粑”是眉山著名特色小吃,产品畅销省内外,现有一个产品销售点在经销时发现:如果每箱产品盈利10元,每天可售出50箱;若每箱产品涨价1元,日销售量将减少2箱.
(1)现该销售点每天盈利600元,同时又要顾客得到实惠,那么每箱产品应涨价多少元?
(2)若该销售点单纯从经济角度考虑,每箱产品应涨价多少元才能获利最高?
相关试题

