【题目】某文教店老板到批发市场选购A,B两种品牌的绘图工具套装,每套A品牌套装进价比B品牌每套套装进价多2.5元,已知用200元购进A种套装的数量是用75元购进B种套装数量的2倍.
(1)求A,B两种品牌套装每套进价分别为多少元?
(2)若A品牌套装每套售价为13元,B品牌套装每套售价为9.5元,店老板决定,购进B品牌的数量比购进A品牌的数量的2倍还多4套,两种工具套装全部售出后,要使总的获利超过120元,则最少购进A品牌工具套装多少套?
参考答案:
【答案】
(1)解:设B种品牌套装每套进价为x元,则A种品牌套装每套进价为(x+2.5)元.
根据题意得: ![]() =2×
=2× ![]() ,
,
解得:x=7.5,
经检验,x=7.5为分式方程的解,
∴x+2.5=10.
答:A种品牌套装每套进价为10元,B种品牌套装每套进价为7.5元.
(2)解:设购进A品牌工具套装a套,则购进B品牌工具套装(2a+4)套,
根据题意得:(13﹣10)a+(9.5﹣7.5)(2a+4)>120,
解得:a>16,
∵a为正整数,
∴a取最小值17.
答:最少购进A品牌工具套装17套.
【解析】(1)此题的等量关系是:每套A品牌套装进价=B品牌每套套装进价+2.5,已知用200元购进A种套装的数量=用75元购进B种套装数量的2倍,设未知数,建立方程求解。
(2)挖掘题中的等量关系是:购进B品牌的数量=购进A品牌的数量的2倍+4;不等关系是:两种工具套装全部售出后,要使总的获利>120,建立不等式求解,再求出不等式的最小整数解即可。
【考点精析】掌握分式方程的应用是解答本题的根本,需要知道列分式方程解应用题的步骤:审题、设未知数、找相等关系列方程、解方程并验根、写出答案(要有单位).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一架梯子长25米,斜靠在一面墙上,梯子底端离墙7米。

(1)这个梯子的顶端离地面有多高?
(2)如果梯子的顶端下滑了4米,那么梯子的底端在水平方向滑动了几米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,P为AD边上一点,沿直线BP将△ABP翻折至△EBP(点A的对应点为点E),PE与CD相交于点O,且OE=OD.
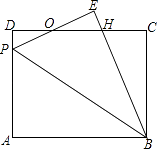
(1)求证:PE=DH;
(2)若AB=10,BC=8,求DP的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A,B两个工厂位于一段直线形河的异侧,A厂距离河边AC=5km,B厂距离河边BD=1km,经测量CD=8km,现准备在河边某处(河宽不计)修一个污水处理厂E.
(1)设ED=x,请用x的代数式表示AE+BE的长;
(2)为了使两厂的排污管道最短,污水厂E的位置应怎样来确定此时需要管道多长?
(3)通过以上的解答,充分展开联想,运用数形结合思想,请你猜想
 的最小值为多少?
的最小值为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在△ABC中,∠B=90°,AB=8cm,BC=6cm,点P从点A开始沿△ABC的边做逆时针运动,且速度为每秒1cm;点Q从点B开始沿△ABC的边做逆时针运动,且速度为每秒2cm,他们同时出发,设运动时间为t秒.

(1)出发2秒后,P,Q两点间的距离为多少cm?
(2)在运动过程中,△PQB能形成等腰三角形吗?若能,请求出几秒后第一次形成等腰三角形;若不能,则说明理由.
(3)出发几秒后,线段PQ第一次把△ABC的周长分成相等两部分?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD,AE,AF分别为△ABC的高线、角平分线和中线.

(1)写出图中所有相等的角和相等的线段;
(2)当BF=8cm,AD=7 cm时,求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD内接于⊙O,点E为AD上一点,连接AC,CB,∠B=∠AEC.
(1)如图1,求证:CE=CD;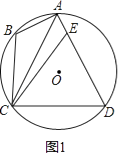
(2)如图2,若∠B+∠CAE=120°,∠ACD=2∠BAC,求∠BAD的度数;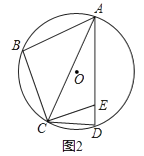
(3)如图3,在(2)的条件下,延长CE交⊙O于点G,若tan∠BAC=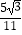 ,EG=2,求AE的长.
,EG=2,求AE的长.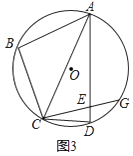
相关试题

