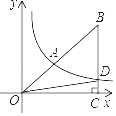
【题目】如图,双曲线y=![]() 经过Rt△BOC斜边上的点A,且满足
经过Rt△BOC斜边上的点A,且满足![]() ,与BC交于点D,S△BOD=21,求:
,与BC交于点D,S△BOD=21,求:
(1)S△BOC
(2)k的值.
参考答案:
【答案】(1)S△BOC=25;(2)k=8
【解析】
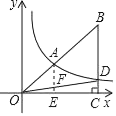
(1)过点A作AE⊥OC于点E,交OD于点F,由平行线分线段成比例可得![]() =
=![]() =
=![]() =
=![]() ,利用面积比是相似比的平方得
,利用面积比是相似比的平方得![]() =
=![]() =
=![]() ,根据反比例函数图象性质得S△AOE=S△ODC,所以
,根据反比例函数图象性质得S△AOE=S△ODC,所以![]() =
=![]() =
=![]() ,进而△BOC的面积.(2) 设A(a,b),由(1)可得S△OCD=4 ,进而可得ab=8,从而求出k的值.
,进而△BOC的面积.(2) 设A(a,b),由(1)可得S△OCD=4 ,进而可得ab=8,从而求出k的值.
解:过点A作AE⊥OC于点E,交OD于点F,
∵AE∥BC, ![]() ,
,
∴![]() =
=![]() =
=![]() =
=![]() ,
,
∴![]() =
=![]() =
=![]() ,
,
∵ S△AOE=S△ODC,
∴![]() =
=![]() =
=![]() ,
,
∴S△BOC=25,
(2)设A(a,b),
∵点A在第一象限,
∴k=ab>0,
∵S△BOC=25,S△BOD=21,
∴S△OCD=4 即![]() ab=4,
ab=4,
∴ab=8,
∴k=8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,对角线AC与BD相交于点O,点E是BC上的一个动点,连接DE, 交 AC于点F.
(1)如图①,当
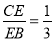 时,求
时,求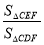 的值;
的值;(2)如图②当DE平分∠CDB时,求证:AF=
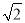 OA;
OA;(3)如图③,当点E是BC的中点时,过点F作FG⊥BC于点G,求证:CG=
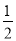 BG.
BG.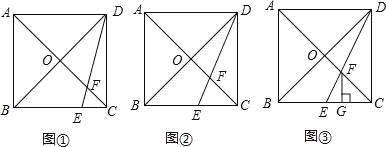
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A(1,4)、B(2,a)在函数y=
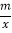 (x>0)的图象上,直线AB与x轴相交于点C,AD⊥x轴于点D.
(x>0)的图象上,直线AB与x轴相交于点C,AD⊥x轴于点D.(1)m= ;
(2)求点C的坐标;
(3)在x轴上是否存在点E,使以A、B、E为顶点的三角形与△ACD相似?若存在,求出点E的坐标;若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下图的数阵由88个偶数排成.现用一个如图所示的平行四边形框可以框出四个数;

①图中平行四边形框内的四个数有什么关系?
②在数阵中任意作一类似(1)中的平行四边形框,设其中左上角的一个数是
 ,那么其他三个数怎样表示?
,那么其他三个数怎样表示?③在这个数阵的平行四边形框内,是否存在和为288的四个数?若存在,求出这四个数;不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OA⊥OC,OB⊥OD,下面结论:①∠AOB=∠COD;②∠AOB+∠COD=90°;③∠BOC+∠AOD=180°;④∠AOC﹣∠COD=∠BOC中,正确的有________(填序号).

-
科目: 来源: 题型:
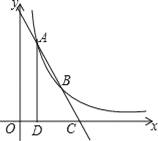
查看答案和解析>>【题目】如图1,在矩形ABCD中,动点E从A出发,沿
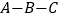 方向运动,当点E到达点C时停止运动,过点E做
方向运动,当点E到达点C时停止运动,过点E做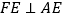 ,交CD于F点,设点E运动路程为x,
,交CD于F点,设点E运动路程为x, 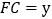 ,如图2所表示的是y与x的函数关系的大致图象,当点E在BC上运动时,FC的最大长度是
,如图2所表示的是y与x的函数关系的大致图象,当点E在BC上运动时,FC的最大长度是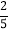 ,则矩形ABCD的面积是( )
,则矩形ABCD的面积是( )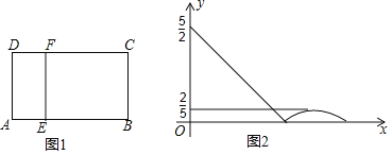
A.
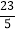 B.
B. 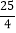 C. 6 D. 5
C. 6 D. 5 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在四边形ABCD中,AB=3CD,AB∥CD,CE∥DA,DF∥CB.
(1)求证:四边形CDEF是平行四边形;
(2)填空:
①当四边形ABCD满足条件 时(仅需一个条件),四边形CDEF是矩形;
②当四边形ABCD满足条件 时(仅需一个条件),四边形CDEF是菱形.
相关试题

