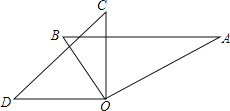
【题目】如图,两块直角三角板的直角顶点O重合在一起,若∠BOC=![]() ∠AOD,则∠BOC的度数为( )
∠AOD,则∠BOC的度数为( )
A.22.5°B.30°C.45°D.60°
参考答案:
【答案】A
【解析】
此题由“两块直角三角板”可知∠DOC=∠BOA=90°,根据同角的余角相等可以证明∠DOB=∠AOC,由题意设∠BOC=x°,则∠AOD=7x°,结合图形列方程即可求解.
解:由两块直角三角板的直顶角O重合在一起可知:∠DOC=∠BOA=90°,
∴∠DOB+∠BOC=90°,∠AOC+∠BOC=90°,
∴∠DOB=∠AOC,
设∠BOC=x°,则∠AOD=7x°,
∴∠DOB+∠AOC=∠AOD﹣∠BOC=6x°,
∴∠DOB=3x°,
∴∠DOB+∠BOC=4x°=90°,
解得:x=22.5.
故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 为直线
为直线 上的一点,
上的一点,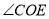 是直角,
是直角, 平分
平分 .
. (1)如图1,若
 =
= °,则
°,则 = °,
= °, 与
与 的数量关系为 .
的数量关系为 .(2)当射线
 绕点
绕点 逆时针旋转到如图2的位置时,(1)中
逆时针旋转到如图2的位置时,(1)中 与
与 的关系是否仍然成立?如成立,请说明理由.
的关系是否仍然成立?如成立,请说明理由.(3)在图3中,若
 =
= °,在
°,在 的内部是否存在一条射线
的内部是否存在一条射线 ,使得
,使得 ?若存在,请求出
?若存在,请求出 的度数;若不存在,请说明理由.
的度数;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道平行四边形有很多性质,现在如果我们把平行四边形沿着它的一条对角线翻折,会发现这其中还有更多的结论.
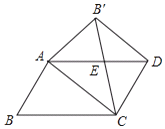
(发现与证明)ABCD中,AB≠BC,将△ABC沿AC翻折至△AB`C,连结B`D.
结论1:△AB`C与ABCD重叠部分的图形是等腰三角形;结论2:B`D∥AC;
(1)请证明结论1和结论2;
(应用与探究)
(2)在ABCD中,已知BC=2,∠B=45°,将△ABC沿AC翻折至△AB`C,连接B`D
 若以A、C、D、B`为顶点的四边形是正方形,求AC的长(要求画出图形)
若以A、C、D、B`为顶点的四边形是正方形,求AC的长(要求画出图形) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A、B、C是直径为6cm的⊙O上的点,且AB=3cm,AC=3
 cm,则∠BAC的度数为( )
cm,则∠BAC的度数为( )A. 15° B. 75°或15° C. 105°或15° D. 75°或105°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,动点S从点A出发,沿线段AB运动至点B后,立即按原路返回,点S在运动过程中速度不变,则以点B为圆心,线段BS长为半径的圆的面积m与点S的运动时间t之间的函数关系图象大致为( )

A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:①两个数互为倒数,则它们乘积为1;②若a、b互为相反数,则
 =﹣1;③两个四次单项式的和一定是四次多项式;④两个有理数比较,绝对值大的反而小;⑤若a为任意有理数,则a﹣|a|≤0;⑥﹣5πR2的系数是﹣5.其中正确的有( )
=﹣1;③两个四次单项式的和一定是四次多项式;④两个有理数比较,绝对值大的反而小;⑤若a为任意有理数,则a﹣|a|≤0;⑥﹣5πR2的系数是﹣5.其中正确的有( )A.2个B.3个C.4个D.5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正五边形的边长为2,连接对角线AD、BE、CE,线段AD分别与BE和CE相交于点M、N,给出下列结论:①∠AME=108°,②AN2=AMAD;③MN=3-
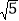 ;④S△EBC=2
;④S△EBC=2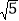 -1,其中正确的结论是_________(把你认为正确结论的序号都填上).
-1,其中正确的结论是_________(把你认为正确结论的序号都填上).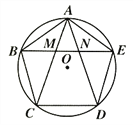
相关试题

