【题目】已知在平面直角坐标系中,抛物线![]() 与x轴相交于点A,B,与y轴相交于点C. 已知A,C两点的坐标分别为A(-4,0), C(0,4).
与x轴相交于点A,B,与y轴相交于点C. 已知A,C两点的坐标分别为A(-4,0), C(0,4).
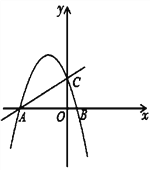
(1)求抛物线的表达式;
(2)如果点P,Q在抛物线上(P点在对称轴左边),且PQ∥AO,PQ=2AO,求P,Q的坐标;
(3)动点M在直线y=x+4上,且△ABC与△COM相似,求点M的坐标.
参考答案:
【答案】(1)![]() ;
;
(2)P点坐标(-5,![]() ),Q点坐标(3,
),Q点坐标(3,![]() );
);
(3)M点的坐标为(![]() ,
,![]() ),(-3,1).
),(-3,1).
【解析】分析:(1)根据待定系数法,可得函数解析式;
(2)根据平行于x轴的直线与抛物线的交点关于对称轴对称,可得P、Q关于直线x=-1对称,根据PQ的长,可得P点的横坐标,Q点的横坐标,根据自变量与函数值的对应关系,可得答案;
(3)根据两组对边对应成比例且夹角相等的两个三角形相似,可得CM的长,根据等腰直角三角形的性质,可得MH的长,再根据自变量与函数值的对应关系,可得答案.
解:(1)将A、C点坐标代入函数解析式,
得 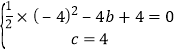 ,
,
解得![]() ,
,
∴抛物线的表达式为![]() ;
;
(2)PQ=2AO=8,
又PQ∥AO,即P、Q关于对称轴x=﹣1对称,
PQ=8,﹣1﹣4=﹣5,
当x=﹣5时,y=![]() ×(-5)2-(-5)+4=
×(-5)2-(-5)+4=![]() ,即P(-5,
,即P(-5,![]() );
);
﹣1+4=3,即Q(3,![]() );
);
P点坐标(-5,![]() ),Q点坐标(3,
),Q点坐标(3,![]() );
);
(3)∠MCO=∠CAB=45°,
①当△MCO∽△CAB时,
![]() ,
,
即![]() ,
,
CM=![]() .
.
如图1,
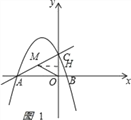
过M作MH⊥y轴于H,
MH=CH=![]() CM=
CM=![]() ,
,
当x=![]() 时,y=
时,y=![]() +4=
+4=![]() ,
,
∴M(![]() ,
,![]() );
);
②当△OCM∽△CAB时,
![]() ,
,
即![]() ,
,
解得CM=![]() ,
,
如图2,
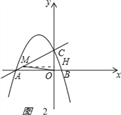
过M作MH⊥y轴于H,MH=CH=![]() CM=3,
CM=3,
当x=﹣3时,y=﹣3+4=1,
∴M(﹣3,1)
综上所述:M点的坐标为(![]() ,
,![]() ),(-3,1).
),(-3,1).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线
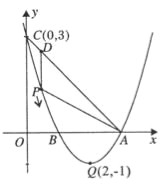
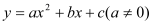 的顶点坐标为Q(2,-1),且与y轴交于点C(0,3),与x轴交于A,B两点(点A在点B的右侧),点P是该抛物线上的一动点,从点C沿抛物线向点A运动(点P与A不重合),过点P作PD∥y轴,交AC于点D.
的顶点坐标为Q(2,-1),且与y轴交于点C(0,3),与x轴交于A,B两点(点A在点B的右侧),点P是该抛物线上的一动点,从点C沿抛物线向点A运动(点P与A不重合),过点P作PD∥y轴,交AC于点D.【1】求该抛物线的函数关系式;
【1】求点P在运动的过程中,线段PD的最大值;
【1】当△ADP是直角三角形时,求点P的坐标;
【1】在题(3)的结论下,若点E在x轴上,点F在抛物线上,问是否存在以A、P、E、F为顶点的平行四边形?若存在,求点F的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将下列各数填在相应的集合里.
﹣
 ,9,0,+4.3,|﹣0.5|,﹣(+7),18%,(﹣3)4,﹣(﹣2)5,﹣62
,9,0,+4.3,|﹣0.5|,﹣(+7),18%,(﹣3)4,﹣(﹣2)5,﹣62正有理数集合:{…};
正分数集合:{…};
负整数集合:{…};
自然数集合:{…}.
-
科目: 来源: 题型:
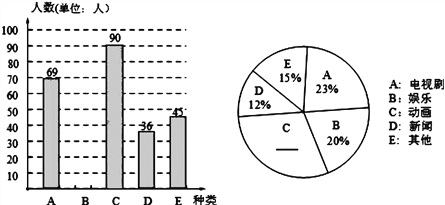
查看答案和解析>>【题目】我市某中学为了了解本校学生对电视节目的喜爱情况,随机调查了部分学生最喜爱哪一类节目(被调查的学生只选一类并且没有不选择的),并将调查结果制成了如下的两个统计图(不完整).请你根据图中所提供的信息,完成下列问题:
(1)求本次调查的学生人数;
(2)请将两个统计图补充完整,并求出新闻节目在扇形统计图中所占圆心角的度数;
(3)若该中学有1500名学生,请估计该校喜爱电视剧节目的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出( )

A.直角三角形的面积
B.最大正方形的面积
C.较小两个正方形重叠部分的面积
D.最大正方形与直角三角形的面积和
-
科目: 来源: 题型:
查看答案和解析>>【题目】反比例函数
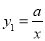 (a>0,a为常数)和
(a>0,a为常数)和 在第一象限内的图象如图所示,点M在
在第一象限内的图象如图所示,点M在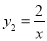 的图象上,MC丄x轴于点C,交
的图象上,MC丄x轴于点C,交 的图象于点A,MD丄y轴于点D,交
的图象于点A,MD丄y轴于点D,交 的图象于点B,当点M在
的图象于点B,当点M在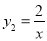 的图象上运动时,以下结论:
的图象上运动时,以下结论:
①S△CDB=S△CCA
②四边形OAMB的面积为2-a
③当a=l时,点A是MC的中点
④若S四边形OAMB+S△CDB,则四边形OCMD为正方形.其中正确是________(把所有正确结论的序号写在横线上)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在等腰三角形ABC中,AB=AC=10,BC=12,D为BC边上的任意一点,过点D分别作DE⊥AB,DF⊥AC,垂足分别为E,F,则DE+DF=______.
相关试题

