【题目】如图,下列判断错误的是( )

A. 如果∠2=∠4,那么AB∥CD B. 如果∠1=∠3,那么AB∥CD
C. 如果∠BAD+∠D=180°,那么AB∥CD D. 如果∠BAD+∠B=180,那么AD∥CD
参考答案:
【答案】B
【解析】
试题分析:根据平行线的判定定理即可求解.
解:A、由内错角相等,两直线平行可知,如果∠2=∠4,那么AB∥CD是正确的,不符合题意;
B、由内错角相等,两直线平行可知,如果∠1=∠3,那么AD∥BC,原来的说法是错误的,符合题意;
C、由同旁内角互补,两直线平行可知,如果∠BAD+∠D=180,那么AB∥CD是正确的,不符合题意;
D、由同旁内角互补,两直线平行可知,如果∠BAD+∠B=180,那么AD∥CD是正确的,不符合题意.
故选B.
-
科目: 来源: 题型:
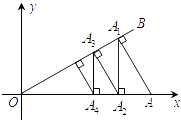
查看答案和解析>>【题目】如图,在平面直角坐标系中,∠AOB=30°,点A坐标为(2,0),过A作AA1⊥OB,垂足为点A1;过点A1作A1A2⊥x轴,垂足为点A2;再过点A2作A2A3⊥OB,垂足为点A3;则A2A3=;再过点A3作A3A4⊥x轴,垂足为点A4…;这样一直作下去,则A2017的纵坐标为 .
-
科目: 来源: 题型:
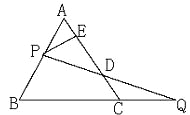
查看答案和解析>>【题目】如图,过边长为1的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,则DE的长为( )
A.
 B.
B.  C.
C.  D. 不能确定
D. 不能确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】在四张编号为A,B,C,D的卡片(除编号外,其余完全相同)的正面分别写上如图所示的正整数后,背面向上,洗匀放好.

(1)我们知道,满足a2+b2=c2的三个正整数a,b,c成为勾股数,嘉嘉从中随机抽取一张,求抽到的卡片上的数是勾股数的概率P1;
(2)琪琪从中随机抽取一张(不放回),再从剩下的卡片中随机抽取一张(卡片用A,B,C,D表示).请用列表或画树形图的方法求抽到的两张卡片上的数都是勾股数的概率P2 , 并指出她与嘉嘉抽到勾股数的可能性一样吗? -
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移,使点A变换为点A′,点B′、C′分别是B、C的对应点.

(1)请画出平移后的△A′B′C′,并求△A′B′C′的面积;
(2)若连接AA′,CC′,则这两条线段之间的关系是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等边三角形,AO⊥BC,垂足为点O,⊙O与AC相切于点D,BE⊥AB交AC的延长线于点E,与⊙O相交于G、F两点.

(1)求证:AB与⊙O相切;
(2)若等边三角形ABC的边长是4,求线段BF的长? -
科目: 来源: 题型:
查看答案和解析>>【题目】两块等腰直角三角板△ABC和△DEC如图摆放,其中∠ACB=∠DCE=90°,F是DE的中点,H是AE的中点,G是BD的中点.
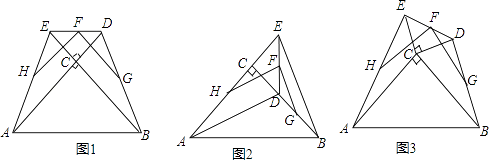
(1)如图1,若点D、E分别在AC、BC的延长线上,通过观察和测量,猜想FH和FG的数量关系为和位置关系为;
(2)如图2,若将三角板△DEC绕着点C顺时针旋转至ACE在一条直线上时,其余条件均不变,则(1)中的猜想是否还成立,若成立,请证明,不成立请说明理由;
(3)如图3,将图1中的△DEC绕点C顺时针旋转一个锐角,得到图3,(1)中的猜想还成立吗?直接写出结论,不用证明.
相关试题

