【题目】如图,点C为线段AB的中点,E为直线AB上方的一点,且满足CE=CB,连接AE,以AE为腰,A为顶角顶点作等腰Rt△ADE,连接CD,当CD最大时,∠DEC的度数为( )
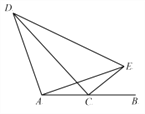
A. 60° B. 75° C. 90° D. 67.5°
参考答案:
【答案】D
【解析】由题意知,当CD⊥CE时,CD取得最大值,此时A、C、E、D共圆,由AC=CE可得∠ADC=∠CDE,从而可求出∠CDE的度数,再根据直角三角形两直角互余求出∠DEC的度数.
:由题意知,当CD⊥CE时,CD取得最大值,此时A、C、E、D共圆.
∵点C为线段AB的中点,
∴AC=BC.
∵CE=CB,
∴AC=CE,
∴∠ADC=∠CDE,
∵∠ADE=45,
∴∠DEC=45÷2=22.5,
∴∠DEC=90-22.5=67.5.
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一个汉字“互”字,其中,AB∥CD,∠1=∠2,∠MGH=∠MEF.

求证:∠MEF=∠GHN.
证明:∵ AB∥CD(已知)
∴∠1=∠3( )
又∵∠1=∠2(已知)
∴∠2=∠3( )
∴ME∥HN ( )
∴∠MGH=∠ ( )( )
又∵∠MGH=∠MEF (已知)
∴∠MEF=∠GHN( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校八年级两个班,各选派10名学生参加学校举行的“建模”大赛预赛,各参赛选手的成绩如下:
八(1)班:88,91,92,93,93,93,94,98,98,100;
八(2)班:89,93,93,93,95,96,96,98,98,99.
通过整理,得到数据分析表如下:
班级
最高分
平均分
中位数
众数
方差
八(1)班
100
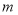
93
93
12
八(2)班
99
95
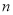
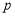
8.4
(1)直接写出表中
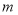 、
、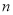 、
、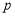 的值为:
的值为: _____,
_____,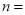 _____,
_____,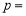 _____;
_____;(2)依据数据分析表,有人说:“最高分在(1)班,(1)班的成绩比(2)班好.”但也有人说(2)班的成绩要好.请给出两条支持八(2)班成绩好的理由;
(3)学校从平均数、中位数、众数、方差中选取确定了一个成绩,等于或大于这个成绩的学生被评定为“优秀”等级,如果八(2)班有一半的学生能够达到“优秀”等级,认为这个成绩应定为_____分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在20km越野赛中,甲乙两选手的行程y(单位:km)随时间x(单位:h)变化的图象
如图所示,根据图中提供的信息,有下列说法:
①两人相遇前,甲的速度小于乙的速度; ②出发后1小时,两人行程均为10km;
③出发后1.5小时,甲的行程比乙多3km; ④甲比乙先到达终点.
其中正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知DC∥FP,∠1=∠2,∠FED=28°,∠AGF=80°,FH平分∠EFG.

(1)证明:DC∥AB;
(2)求∠PFH的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰直角
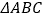 中,
中,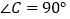 ,
,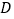 为
为 的中点,将
的中点,将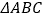 折叠,使点
折叠,使点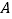 与点
与点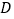 重合,
重合,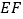 为折痕,则
为折痕,则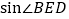 的值是( )
的值是( )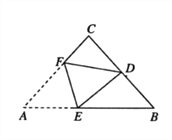
A.
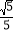 B.
B. 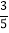 C.
C. 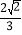 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠ABD、∠ACD的角平分线交于点P,若∠A=50°,∠D=10°,则∠P的度数为( )
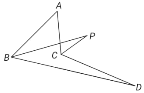
A. 10°B. 15°C. 20°D. 25°
相关试题

