【题目】如图,以△ABC的三边为边,在BC的同侧分别作3个等边三角形,即△ABD、△BCE、△ACF.

(1)求证:四边形ADEF是平行四边形?
(2)当△ABC满足什么条件时,四边形ADEF是矩形,并说明理由.
(3)当△ABC满足什么条件时,边形ADEF是菱形,并说明理由.
(4)当△ABC满足什么条件时,四边形ADEF是正方形,不要说明理由.
参考答案:
【答案】(1)见解析;(2)当∠BAC=150°时,四边形ADEF是矩形;(3)AB=AC时,四边形ADEF是菱形;(4)∠BAC=150°时,四边形ADEF是正方形.
【解析】
试题分析:(1)可先证明△ABC≌△DBE,可得DE=AC,又有AC=AF,可得DE=AF,同理可得AD=EF,根据两组对边分别相等的四边形是平行四边形,可证四边形ADEF是平行四边形;
(2)如四边形ADEF是矩形,则∠DAF=90°,又有∠BAD=∠FAC=60°,可得∠BAC=150°,故∠BAC=150°时,四边形ADEF是矩形;
(3)若四边形ADEF是菱形,则AD=AF,所以AB=AC,则△ABC是等腰三角形;
(4)若四边形ADEF是正方形,则AD=AF,且∠DAF=90°,所以△ABC是等腰三角形,且∠BAC=150°.
证明:(1)∵△ABD,△BCE都是等边三角形,
∴∠DBE=∠ABC=60°﹣∠ABE,AB=BD,BC=BE.
在△ABC与△DBE中,
 ,
,
∴△ABC≌△DBE(SAS).
∴DE=AC.
又∵AC=AF,
∴DE=AF.
同理可得EF=AD.
∴四边形ADEF是平行四边形.
(2)∵四边形ADEF是平行四边形,
∴当∠DAF=90°时,四边形ADEF是矩形,
∴∠FAD=90°.
∴∠BAC=360°﹣∠DAF﹣∠DAB﹣∠FAC=360°﹣90°﹣60°﹣60°=150°.
则当∠BAC=150°时,四边形ADEF是矩形;
(3)∵四边形ADEF是平行四边形,
∴当AD=AF时,四边形ADEF是菱形,
又∵AD=AB,AF=AC,
∴AB=AC时,四边形ADEF是菱形;
(4)综合(2)、(3)知,当△ABC是等腰三角形,且∠BAC=150°时,四边形ADEF是正方形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一个等腰三角形的两条边的长为4和5,则这个等腰三角形的周长为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】买一个篮球需要x元,买一个排球需要y元,买一个足球需要z元,买5个篮球、3个排球、2个足球共需要___________元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于
 ,
,  的方程组
的方程组
(1)请写出方程
 的所有正整数解;
的所有正整数解;(2)若方程组的解满足
 ,求
,求 的值;
的值;(3)无论实数
 取何值,方程
取何值,方程 总有一个公共解,你能把求出这个公共解吗?
总有一个公共解,你能把求出这个公共解吗?(4)如果方程组有整数解,求整数
 的值。
的值。 -
科目: 来源: 题型:
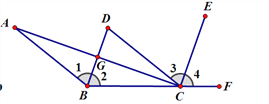
查看答案和解析>>【题目】如图,CD//AB,BD平分∠ABC,CE平分∠DCF,∠ACE=90°
(1)请问BD和CE是否平行?请你说明理由;
(2)AC和BD有何位置关系?请你说明判断的理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】三角形内有一点到三角形三边的距离相等,则这个点一定是三角形的( )
A. 三条高的交点 B. 三条角平分线的交点
C. 三边中线的交点 D. 三边垂直平分线的交点
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列条件中,不能够判定一个四边形是平行四边形的是( )
A. 一组对边平行,另一组对边相等 B. 一组对边平行且相等
C. 两组对边分别平行 D. 对角线互相平分
相关试题

