【题目】已知关于![]() ,
, ![]() 的方程组
的方程组![]()
(1)请写出方程![]() 的所有正整数解;
的所有正整数解;
(2)若方程组的解满足![]() ,求
,求![]() 的值;
的值;
(3)无论实数![]() 取何值,方程
取何值,方程![]() 总有一个公共解,你能把求出这个公共解吗?
总有一个公共解,你能把求出这个公共解吗?
(4)如果方程组有整数解,求整数![]() 的值。
的值。
参考答案:
【答案】(1) ![]() ;
; ![]() ;(2)
;(2) ![]() ;(3)x=0,y=
;(3)x=0,y=![]() ;(4)2或-6.
;(4)2或-6.
【解析】试题分析:(1)由题意求方程的解且要使x,y都是正整数,将方程移项,再把x和y互相表示出来,在由题意要求x>0,y>0,根据以上两个条件可夹出合适的x值,从而代入方程得到相应的y值;
(2)由方程组![]() 求得x,y的值,代入方程
求得x,y的值,代入方程![]() 即可求得m的值;
即可求得m的值;
(3)方程整理后,根据无论m如何变化,二元一次方程总有一个固定的解,列出方程组,求出方程组的解即可.
(4)先把m当作已知求出x、y的值,再根据方程组有正整数解,进行判断,再找出符合条件的正整数m的值即可.
试题解析(1)由已知方程x+2y=5,移项得x=5-2y,
∵x,y都是正整数,则有x=5-2y>0,又∵x>0,
∴0<y<2.5,
又∵y为正整数,根据以上条件可知,合适的y值只能是y=1、2,
代入方程得相应x=3、1,
∴方程2x+y=5的正整数解为![]() ;
; ![]()
(2) ∵x+y=0
∴x+2y=5变为y=5
∴x=-5
将![]() 代入
代入![]() 得
得![]() .
.
(3) ∵由题意得二元一次方程![]() 总有一个公共解
总有一个公共解
∴方程变为(m+1)x-2y+9=0
∵这个解和m无关,
∴x=0,y=![]()
(4) 将方程组![]() 两个方程相加得
两个方程相加得![]()
∴![]()
∵方程组有整数解且m为整数
∴![]() ,
, ![]() ,
, ![]()
①m+2=1,计算得: 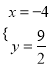 (不符合题意)
(不符合题意)
②m+2=-1,计算得: ![]() (不符合题意)
(不符合题意)
③m+2=2,计算得: 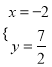 (不符合题意)
(不符合题意)
④m+2=-2,计算得: ![]() (不符合题意)
(不符合题意)
⑤m+2=4,计算得: ![]() (不符合题意)∴m=2
(不符合题意)∴m=2
⑥ m+2=-4,计算得: ![]() (不符合题意)∴m=-6
(不符合题意)∴m=-6
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下列各组线段长为边能组成三角形的是( )
A. 5cm,6cm,12cm B. 2cm,4cm,6cm C. 1cm,2cm,4cm D. 4cm,6cm,8cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个等腰三角形的两条边的长为4和5,则这个等腰三角形的周长为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】买一个篮球需要x元,买一个排球需要y元,买一个足球需要z元,买5个篮球、3个排球、2个足球共需要___________元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以△ABC的三边为边,在BC的同侧分别作3个等边三角形,即△ABD、△BCE、△ACF.

(1)求证:四边形ADEF是平行四边形?
(2)当△ABC满足什么条件时,四边形ADEF是矩形,并说明理由.
(3)当△ABC满足什么条件时,边形ADEF是菱形,并说明理由.
(4)当△ABC满足什么条件时,四边形ADEF是正方形,不要说明理由.
-
科目: 来源: 题型:
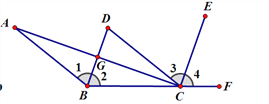
查看答案和解析>>【题目】如图,CD//AB,BD平分∠ABC,CE平分∠DCF,∠ACE=90°
(1)请问BD和CE是否平行?请你说明理由;
(2)AC和BD有何位置关系?请你说明判断的理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】三角形内有一点到三角形三边的距离相等,则这个点一定是三角形的( )
A. 三条高的交点 B. 三条角平分线的交点
C. 三边中线的交点 D. 三边垂直平分线的交点
相关试题

