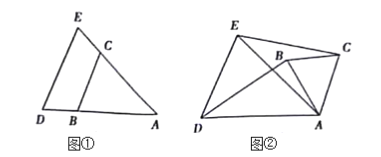
【题目】如图①,在△ABC与△ADE中,AB=AC,AD=AE,∠A是公共角。
(1)BD与CE的数量关系是:BD______CE;
(2)把图①△ABC绕点A旋转一定的角度,得到如图②所示的图形。
①求证:BD=CE;
②BD与CE所在直线的夹角与∠DAE的数量关系是什么?说明理由。
(3)若AD=10,AB=6,把图①中的△ABC绕点A顺时针旋转α度(0°<α≤360)直接写出BD长度的取值范围。
参考答案:
【答案】(1)=;(2)见解析;(3)4≤BD≤16.
【解析】试题分析:(1)由线段的和差即可得到结论;
(2)①由旋转的性质得到∠DAE=∠BAC,进而得到∠BAD=∠CAE.然后证明△ABD≌△ACE,再由全等三角形的对应边相等即可得到结论;
②延长DB交CE于点F.由全等三角形对应角相等,得到∠ADB=∠AEC,再由三角形内角和定理即可得到结论;
③当B在线段DA上时,DB最短,当B在DA的延长线上时,DB最长,由此即可得出结论.
试题解析:解:(1)=.理由如下:
∵AB=AC,AD=AE,∴AD- AB =AE –AC,∴BD=CE;
(2)①由旋转的性质得到:∠DAE=∠BAC,∴∠DAE+∠BAE=∠BAC+∠BAE,即∠BAD=∠CAE.在△ABD和△ACE中,∵AB=AC,∠BAD=∠CAE,AD=AE,∴△ABD≌△ACE(SAS),∴BD=CE.
②BD与CE所在直线的夹角与∠DAE的度数相等.延长DB交CE于点F.

∵△ABD≌△ACE,∴∠ADB=∠AEC.
又∵∠AOD=∠EOF,∴180°-∠ADB-∠AOD =180°-∠AEC-∠EOF,即∠DAE=∠DFE.
③当B在线段DA上时,DB=DA-BA=4最短;当B在DA的延长线上时,DB=DA+BA=16最长.故4≤BD≤16.
-
科目: 来源: 题型:
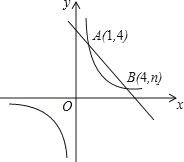
查看答案和解析>>【题目】如图,一次函数y=kx+b与反比例函数y=
 的图象交于A(1,4),B(4,n)两点.
的图象交于A(1,4),B(4,n)两点.(1)求反比例函数和一次函数的解析式;
(2)点P是x轴上的一动点,试确定点P并求出它的坐标,使PA+PB最小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,为探测某座山的高度AB,某飞机在空中C处测得山顶A处的俯角为31°,此时飞机的飞行高度为CH=4千米;保持飞行高度与方向不变,继续向前飞行2千米到达D处,测得山顶A处的俯角为50°,求此山的高度AB.(参考数据:tan31°≈0.6,1an50°≈1.2)

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校计划购买篮球、排球共20个,购买2个篮球,3个排球,共需花费190元;购买3个篮球的费用与购买5个排球的费用相同。
(1)篮球和排球的单价各是多少元?
(2)若购买篮球不少于8个,所需费用总额不超过800元.请你求出满足要求的所有购买方案,并直接写出其中最省钱的购买方案
-
科目: 来源: 题型:
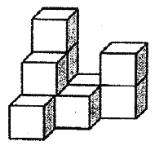
查看答案和解析>>【题目】根据要求完成下列题目
(1)图中有______块小正方体;
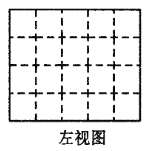
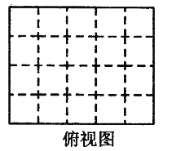
(2)请在下面方格纸中分别画出它的主视图、左视图和俯视图;
(3)用小正方体搭一几何体,使得它的俯视图和主视图与你在上图方格中所画的图一致,若这样的几何体最少要个
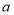 小正方体,最多要
小正方体,最多要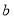 个小正方体,则
个小正方体,则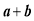 的值为___________.
的值为___________.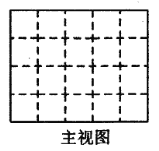
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正n边形的周长为60,边长为a
(1)当n=3时,请直接写出a的值;
(2)把正n边形的周长与边数同时增加7后,假设得到的仍是正多边形,它的边数为n+7,周长为67,边长为b.有人分别取n等于3,20,120,再求出相应的a与b,然后断言:“无论n取任何大于2的正整数,a与b一定不相等.”你认为这种说法对吗?若不对,请求出不符合这一说法的n的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,用三个正方形①、2个正方形②、1个正方形③和缺了一个角的长方形④,恰好拼成一个大长方形.根据图示数据,解答下列问题:
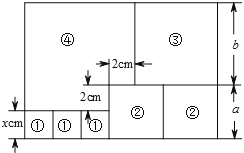
(1)用含x的代数式表示:a=__________cm,b=__________cm;
(2)用含x的代数式表示大长方形的周长,并求x=5时大长方形的周长.
相关试题

