【题目】一次函数y=kx+b经过点(-1,1)和点(2,7).
(1)求这个一次函数的解析表达式.
(2)将所得函数图象平移,使它经过点(2,-1),求平移后直线的解析式.
参考答案:
【答案】
(1)解:将点(-1,1)和点(2,7)代入解析式得:![]() ,
,
解得: ![]() ,
,
∴一次函数的解析表达式为:y=2x+3
(2)解:因为平移,所以直线平行,所以设y=2x+b ,
把点(2,-1)代入,得b=-5,
∴平移后直线的解析式为:y=2x-5
【解析】(1)设函数解析式,利用待定系数法建立方程组。解方程组求出k、b的值,再写出函数解析式即可。
(2)根据平移的性质可知两一次函数的图像平行,则k的值相等,因此设平移后的一次函数解析式为y=2x+b,再将(2,-1)代入建立方程求出b的值,就可以得出函数解析式。
【考点精析】本题主要考查了确定一次函数的表达式的相关知识点,需要掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一组数据x1 , x2 , …,xn的方差是s2 , 则新的一组数据ax1+1,ax2+1,…,axn+1(a为非零常数)的方差是(用含a和s2的代数式表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=kx+b的图象经过点(3,5)与(-4,-9).
(1)求这个一次函数的解析式;
(2)求关于x的不等式kx+b≤5的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】在四张编号为A,B,C,D的卡片(除编号外,其余完全相同)的正面分别写上如图所示的正整数后,背面向上,洗匀放好.

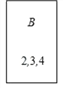


(1)从中随机抽取一张,若以卡片上的数字作为三角形的三边长,能构成三角形的概率为
(2)先从中随机抽取一张(不放回),再从剩下的卡片中随机抽取一张,请用列表或画树形图的方法求抽到的两张卡片上的数都是勾股数的概率(满足a2+b2=c2的三个正整数a,b,c成为勾股数)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件属于随机事件的是( )
A.明天的早晨,太阳从东方升起B.13人中至少有两人同生肖
C.抛出一枚骰子,点数为0D.打开电视机,正在播放广告
-
科目: 来源: 题型:
查看答案和解析>>【题目】若点A(m,n)在第二象限,那么点B(﹣m,|n|)在( )
A.第一象限
B.第二象限;
C.第三象限
D.第四象限 -
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:[(3x+2y)(3x﹣2y)﹣(x+2y)(3x﹣2y)]÷x,其中x=2,y=﹣1.6
相关试题

