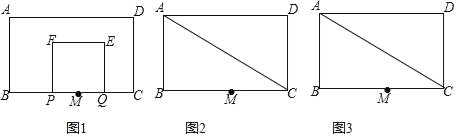
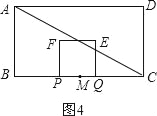
【题目】如图,在矩形ABCD中,AB=3,BC=4,点M是BC的中点,点P从点M出发沿MB以每秒1个单位的速度向点B匀速运动,到达点B后立刻以原速度沿BM返回;同时点Q从点M出发以每秒1个单位长的速度在射线MC上匀速运动,在点P,Q的运动过程中,以PQ为边作正方形PQEF,使它与矩形ABCD在BC的同侧,点P,Q同时出发,当点P返回点M时,则两点停止运动,设点P,Q运动的时间是t秒(t>0).
(1)当点P运动到BM的中点时,t= ;
(2)设正方形PQEF与矩形ABCD重叠部分的面积为S,直接写出S与t之间的函数关系式及t的取值范围;
(3)连结AC,当正方形PQEF与△ADC重叠部分为三角形时,求t的取值范围.
参考答案:
【答案】(1)1或3;(2)①S=4t2;②S=6t;③S=﹣3t+18;(3)![]() <t≤
<t≤![]() 或t=2
或t=2
【解析】分析:(1)求出BM=![]() BC=2,当点P第一次运动到BM的中点时,PM=
BC=2,当点P第一次运动到BM的中点时,PM=![]() BM=1,得出t=1;当点P第二次运动到BM的中点时,运动的路程=3,得出t=3即可;
BM=1,得出t=1;当点P第二次运动到BM的中点时,运动的路程=3,得出t=3即可;
(2)分为三种情况:①当0<t≤1.5时,PQ=2t,由正方形面积公式即可得出答案;
②当1.5<t≤2时得出PQ=2t,AB=3,由矩形面积即可得出答案;
③当2<t≤4时,求出PC=6-t,AB=3,由矩形面积即可得出答案;
(3)当点E在AC上时,得出△CEQ∽△CAB,得出对应边成比例,即可得出t的值;当F在AC上时,△CPF∽△CBA,得出对应边成比例,即可得出t的值;当点F在EA的延长线上时,点E在CD的延长线上,此时t=2;即可得出答案.
详解:(1)∵BC=4,点M是BC的中点,
∴BM=![]() BC=2,
BC=2,
当点P第一次运动到BM的中点时,PM=![]() BM=1,
BM=1,
∴t=1;
当点P第二次运动到BM的中点时,运动的路程=2+1=3,
∴t=3;
故答案为:1或3;
(2)分为三种情况:
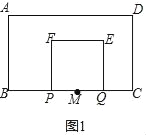
①如图1,当0<t≤1.5时,
∵PQ=2t,
∴S=(2t)2,
∴S=4t2;
②如图2,
当1.5<t≤2时,
∵PQ=2t,AB=3,
∴S=6t;
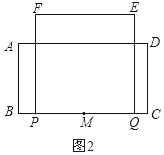
③如图3,
当2<t≤4时,
∵PC=6﹣t,AB=3,
∴S=﹣3t+18;
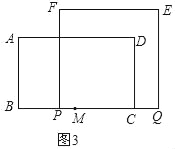
(3)如图4,
当点E在AC上时,
∵△CEQ∽△CAB,
∴![]() ,
,
∴![]() ,
,
∴t=![]() ,
,
当F在AC上时,
∵△CPF∽△CBA,
∴![]() ,
,
∴![]() ,
,
∴t=![]() ;当点F在EA的延长线上时,点E在CD的延长线上,此时t=2;
;当点F在EA的延长线上时,点E在CD的延长线上,此时t=2;
∴t的取值范围是![]() <t≤
<t≤![]() 或t=2.
或t=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程
 .
.(1)求证:对于任意实数m,方程总有两个不相等的实数根;
(2)若方程的一个根是1,求m的值及方程的另一个根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司开发了一种新产品,现要在甲地或者乙地进行销售,设年销售量为x(件),其中x>0.
若在甲地销售,每件售价y(元)与x之间的函数关系式为y=﹣
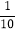 x+100,每件成本为20元,设此时的年销售利润为w甲(元)(利润=销售额﹣成本).
x+100,每件成本为20元,设此时的年销售利润为w甲(元)(利润=销售额﹣成本).若在乙地销售,受各种不确定因素的影响,每件成本为a元(a为常数,18≤a≤25 ),每件售价为98元,销售x(件)每年还需缴纳
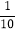 x2元的附加费.设此时的年销售利润为w乙(元)(利润=销售额﹣成本﹣附加费).
x2元的附加费.设此时的年销售利润为w乙(元)(利润=销售额﹣成本﹣附加费).(1)当a=18,且x=100是,w乙= 元;
(2)求w甲与x之间的函数关系式(不必写出x的取值范围),当w甲=15000时,若使销售量最大,求x的值;
(3)为完成x件的年销售任务,请你通过分析帮助公司决策,应选择在甲地还是在乙地销售才能使该公司所获年利润最大.
-
科目: 来源: 题型:
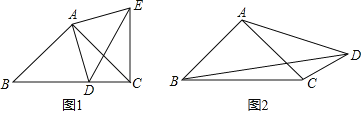
查看答案和解析>>【题目】(1)如图1,在Rt△ABC和Rt△ADE中,AB=AC,AD=AE,且点D在BC边上滑动(点D不与点B,C重合),连接EC,
①则线段BC,DC,EC之间满足的等量关系式为 ;
②求证:BD2+CD2=2AD2;
(2)如图2,在四边形ABCD中,∠ABC=∠ACB=∠ADC=45°.若BD=9,CD=3,求AD的长.
-
科目: 来源: 题型:
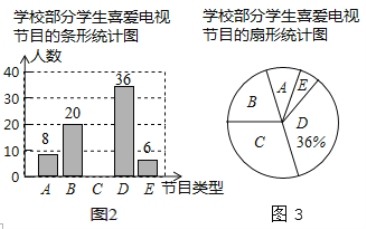
查看答案和解析>>【题目】为了了解本校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,课题小组随机选取该校部分学生进行了问卷调査(问卷调査表如图1所示),并根据调查结果绘制了图2、图3两幅统计图(均不完整),请根据统计图解答下列问题.
(1)本次接受问卷调查的学生有________名.
(2)补全条形统计图.
(3)扇形统计图中B类节目对应扇形的圆心角的度数为________.
(4)该校共有2000名学生,根据调查结果估计该校最喜爱新闻节目的学生人数.

-
科目: 来源: 题型:
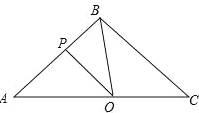
查看答案和解析>>【题目】如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿着AB以每秒4cm的速度向B点运动;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x秒.
(1)当x为何值时,PQ∥BC;
(2)当
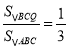 时,求
时,求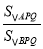 的值;
的值;(3)△APQ能否与△CQB相似?若能,求出时间x的值;若不能,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,四边形OABC的顶点O是坐标原点,点A在第一象限,点C在第四象限,点B在x轴的正半轴上.∠OAB=90°且OA=AB,OB,OC的长分别是二元一次方程组
 的解(OB>OC).
的解(OB>OC).
(1)求点A和点B的坐标;
(2)点P是线段OB上的一个动点(点P不与点O,B重合),过点P的直线l与y轴平行,直线l交边OA或边AB于点Q,交边OC或边BC于点R.设点P的横坐标为t,线段QR的长度为m.已知t=4时,直线l恰好过点C.
①当0<t<3时,求m关于t的函数关系式;
②当m=
 时,求点P的横坐标t的值.
时,求点P的横坐标t的值.
相关试题

