【题目】如图,在正方形ABCD外侧作直线DE,点C关于直线DE的对称点为M,连接CM,AM,其中AM交直线DE于点N.若45°<∠CDE<90°,当MN=3,AN=4时,正方形ABCD的边长为( )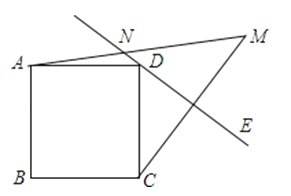
A.![]()
B.5
C.5![]()
D.![]()
![]()
参考答案:
【答案】D
【解析】解:如图所示,连接CN、DM、AC,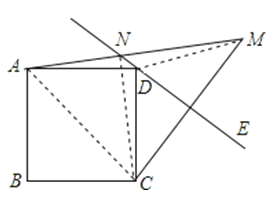
∵点C关于直线DE的对称点为M,
∴CN=MN,CD=DM,∠DCN=∠DMN,
在正方形ABCD中,AD=CD,
∴AD=DM,
∴∠DAM=∠DMN,
∴∠DCN=∠DAM,
∵∠ACN+∠CAN=∠BCD﹣∠DCN+∠CAD+∠DAM=∠BCD+∠CAD=90°,
∴∠ANC=180°﹣90°=90°,
∴△ACN是直角三角形,
由勾股定理得,AC=![]() =5,
=5,
∴正方形ABCD的边长= ![]() .
.
故选D.
【考点精析】掌握正方形的性质是解答本题的根本,需要知道正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
-
科目: 来源: 题型:
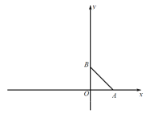
查看答案和解析>>【题目】平面直角坐标系中,点A、B分别在x轴正半轴、y轴正半轴上,AO=BO,△ABO的面积为8.
(1)求点A的坐标;
(2)点C、D分别在x轴负半轴、y轴正半轴上(D在B点上方),AB⊥CD于E,设点D纵坐标为t,△BCE的面积为S,求S与t的函数关系;
(3)在(2)的条件下,点F为BE中点,连接OF交BC于G,当∠FOB+∠DAE=45°时,求点E坐标.


-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,在平面直角坐标系中,点A(o,m),点B(n,0),m, n满足
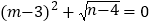 .
.(1)求A,B的坐标.
(2)如图1, E为第二象限内直线AB上的一点,且满足
 ,求点E的横坐标.
,求点E的横坐标.(3)如图2,平移线段BA至OC, B与O是对应点,A与C是对应点,连接AC, E为BA的延长线上一点,连接EO, OF平分∠COE, AF平分∠EAC, OF交AF于点F,若∠ABO+∠OEB=α,请在图2中将图形补充完整,并求∠F (用含α的式子表示)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,对角线AC,BD相交于点O,则图中的等腰直角三角形有( )
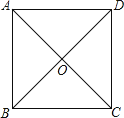
A.4个
B.6个
C.8个
D.10个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中∠DAE=25°,AE交对角线BD于E点,那么∠BEC等于( )

A.45°
B.60°
C.70°
D.75° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD的外侧,作等边△ADE,则∠BED的度数是 .
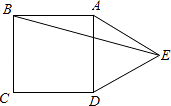
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形ABCD为菱形,其边长为6,
 ,点P在菱形的边AD、CD及对角线AC上运动,当
,点P在菱形的边AD、CD及对角线AC上运动,当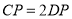 时,则DP的长为________.
时,则DP的长为________.
相关试题

