【题目】已知,在平面直角坐标系中,点A(o,m),点B(n,0),m, n满足![]() .
.
(1)求A,B的坐标.
(2)如图1, E为第二象限内直线AB上的一点,且满足![]() ,求点E的横坐标.
,求点E的横坐标.
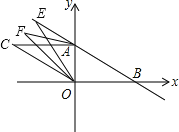
(3)如图2,平移线段BA至OC, B与O是对应点,A与C是对应点,连接AC, E为BA的延长线上一点,连接EO, OF平分∠COE, AF平分∠EAC, OF交AF于点F,若∠ABO+∠OEB=α,请在图2中将图形补充完整,并求∠F (用含α的式子表示)

参考答案:
【答案】(1)A(0,3),B(4,0);(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据非负数的性质列式求出m、n的值,然后写出点A、B的坐标即可;
(2)设点E的横坐标为a,然后利用三角形的面积列式求出a的值,再利用待定系数法求出直线AB的解析式,然后求解即可;
(3)根据平移的性质可得AB∥OC,AC∥OB,根据平行线的性质可得∠OEB=∠COE,∠CAE=∠ABO,然后根据角平分线的定义可得![]() ,
,![]() ,再根据三角形的内角和定理列式整理即可得解.
,再根据三角形的内角和定理列式整理即可得解.
解:(1)由非负数的性质得,m-3=0,n-4=0,
解得m=3,n=4,
所以,A(0,3)B(4,0);
(2)设点E的横坐标为a,
![]() ,
,
![]() ,
,
解得a=![]() ,
,
设直线AB的解析式为y=kx+b,
则![]()
解得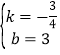
所以,直线AB的解析式为![]() ,
,
当![]() 时,
时,![]() ,
,
所以,点E的坐标为![]() ;
;
(3)由平移的性质,AB∥OC,AC∥OB,
∴∠OEB=∠COE,∠CAE=∠ABO,
∵OF平分∠COE,AF平分∠EAC,
![]() ,
,
由三角形的内角和定理,∠OEB+∠EAF=∠F+∠EOF,
![]() ,
,
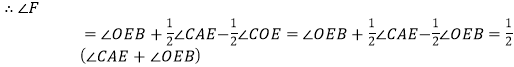 ,
,
∵∠ABO+∠OEB=α,
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若分式
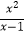 □
□ 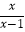 运算结果为x,则在“□”中添加的运算符号为( )
运算结果为x,则在“□”中添加的运算符号为( )
A.+
B.﹣
C.+或×
D.﹣或÷ -
科目: 来源: 题型:
查看答案和解析>>【题目】设A=
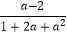 ÷(a﹣
÷(a﹣ 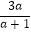 ).
).
(1)化简A;
(2)当a=3时,记此时A的值为f(3);当a=4时,记此时A的值为f(4);… 解关于x的不等式: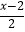 ﹣
﹣ 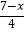 ≤f(3)+f(4)+…+f(11),并将解集在数轴上表示出来.
≤f(3)+f(4)+…+f(11),并将解集在数轴上表示出来.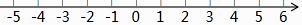
-
科目: 来源: 题型:
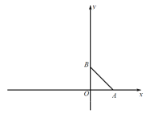
查看答案和解析>>【题目】平面直角坐标系中,点A、B分别在x轴正半轴、y轴正半轴上,AO=BO,△ABO的面积为8.
(1)求点A的坐标;
(2)点C、D分别在x轴负半轴、y轴正半轴上(D在B点上方),AB⊥CD于E,设点D纵坐标为t,△BCE的面积为S,求S与t的函数关系;
(3)在(2)的条件下,点F为BE中点,连接OF交BC于G,当∠FOB+∠DAE=45°时,求点E坐标.


-
科目: 来源: 题型:
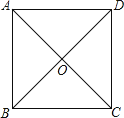
查看答案和解析>>【题目】如图,正方形ABCD中,对角线AC,BD相交于点O,则图中的等腰直角三角形有( )
A.4个
B.6个
C.8个
D.10个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD外侧作直线DE,点C关于直线DE的对称点为M,连接CM,AM,其中AM交直线DE于点N.若45°<∠CDE<90°,当MN=3,AN=4时,正方形ABCD的边长为( )
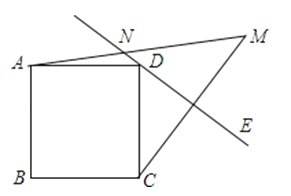
A.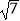
B.5
C.5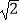
D.
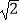
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中∠DAE=25°,AE交对角线BD于E点,那么∠BEC等于( )

A.45°
B.60°
C.70°
D.75°
相关试题

