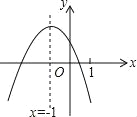
【题目】二次函数y=ax2+bx+c（a≠0）如图所示，下列结论中：

①4ac-b2＜0；②3b+2c＜0；③4a+c＜2b；④m（am+b）+b＜a（m≠-1）．

其中正确的结论有（ ）

A．1个 B．2个 C．3个 D．4个

参考答案：

【答案】C.

【解析】

试题解析：∵图象与x轴有两个交点，

∴b2-4ac＞0，

所以①正确；

∵图象的对称轴为直线x=-1，

∴-=-1，解得b=2a，

∵从图象可知，当x=1时，y＜0，

∴a+b+c＜0 2a+2b+2c＜0 3b+2c＜0， 所以②正确；

∵图象的对称轴为直线x=-1，当x=0时，y=c＞0

∴当x=-2时，y＞0

∴4a-2b+c＞0,则有4a+c＞2b

所以③错误；

由式子④整理得am2+bm+b-a＜0

把b=2a代入得am2+2am+a＜0

在不等式两边都除以a，由于抛物线开口向下，故a＜0，则不等号方向应改变，整理得

m2+2m+1＞0配方得（m+1）2＞0

∵m≠-1

∴（m+1）2＞0成立

所以④正确．

故选C．

关闭