【题目】如图,在菱形ABCD中,AB=6,∠ABC=60°,AH⊥BC于点H.动点E从点B出发,沿线段BC向点C以每秒2个单位长度的速度运动.过点E作EF⊥AB,垂足为点F.点E出发后,以EF为边向上作等边三角形EFG,设点E的运动时间为t秒,△EFG和△AHC的重合部分面积为S.
(1)CE= (含t的代数式表示).
(2)求点G落在线段AC上时t的值.
(3)当S>0时,求S与t之间的函数关系式.
(4)点P在点E出发的同时从点A出发沿A-H-A以每秒2![]() 个单位长度的速度作往复运动,当点E停止运动时,点P随之停止运动,直接写出点P在△EFG内部时t的取值范围.
个单位长度的速度作往复运动,当点E停止运动时,点P随之停止运动,直接写出点P在△EFG内部时t的取值范围.

参考答案:
【答案】(1)6-2t;(2)t=2;(3)当![]() <t≤2时,S=
<t≤2时,S=![]() t2+
t2+![]() t-3
t-3![]() ;当2<t≤3时,S=-
;当2<t≤3时,S=-![]() t2+
t2+![]() t-
t-![]() ;(4)
;(4)![]() <t<
<t<![]() .
.
【解析】
试题分析: (1)由菱形的性质得出BC=AB=6得出CE=BC-BE=6-2t即可;
(2)由菱形的性质和已知条件得出△ABC是等边三角形,得出∠ACB=60°,由等边三角形的性质和三角函数得出∠GEF=60°,GE=EF=BEsin60°=![]() t,证出∠GEC=90°,由三角函数求出CE=
t,证出∠GEC=90°,由三角函数求出CE=![]() =t,由BE+CE=BC得出方程,解方程即可;
=t,由BE+CE=BC得出方程,解方程即可;
(3)分两种情况:①当![]() <t≤2时,S=△EFG的面积-△NFN的面积,即可得出结果;
<t≤2时,S=△EFG的面积-△NFN的面积,即可得出结果;
②当2<t≤3时,由①的结果容易得出结论;
(4)由题意得出t=![]() 时,点P与H重合,E与H重合,得出点P在△EFG内部时,t的不等式,解不等式即可.
时,点P与H重合,E与H重合,得出点P在△EFG内部时,t的不等式,解不等式即可.
试题解析:(1)根据题意得:BE=2t,
∵四边形ABCD是菱形,
∴BC=AB=6,
∴CE=BC-BE=6-2t;
(2)点G落在线段AC上时,如图1所示:
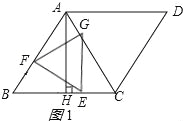
∵四边形ABCD是菱形,
∴AB=BC,
∵∠ABC=60°,
∴△ABC是等边三角形,
∴∠ACB=60°,
∵△EFG是等边三角形,
∴∠GEF=60°,GE=EF=BEsin60°=![]() t,
t,
∵EF⊥AB,
∴∠BEF=90°-60°=30°,
∴∠GEB=90°,
∴∠GEC=90°,
∴CE=![]() =t,
=t,
∵BE+CE=BC,
∴2t+t=6,
解得:t=2;
(3)分两种情况:①当![]() <t≤2时,如图2所示:
<t≤2时,如图2所示:
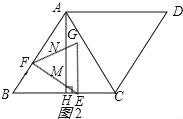
S=△EFG的面积-△NFN的面积=![]() ×
×![]() ×(
×(![]() t)2-
t)2-![]() ×
×![]() ×(-
×(-![]() +2
+2![]() )2=
)2=![]() t2+
t2+![]() t-3
t-3![]() ,
,
即S=![]() t2+
t2+![]() t-3
t-3![]() ;
;
当2<t≤3时,如图3所示:

S=![]() t2+
t2+![]() t-3
t-3![]() -
-![]() (3
(3![]() t-6
t-6![]() )2,
)2,
即S=-![]() t2+
t2+![]() t-
t-![]() ;
;
(4)∵AH=ABsin60°=6×![]() =3
=3![]() ,3
,3![]() ÷2
÷2![]() =
=![]() ,3÷2=
,3÷2=![]() ,
,
∴t=![]() 时,点P与H重合,E与H重合,
时,点P与H重合,E与H重合,
∴点P在△EFG内部时,![]() -
-![]() <(t-
<(t-![]() )×2
)×2![]() <
<![]() t-
t-![]() (2t-3)+
(2t-3)+![]() (2t-3),
(2t-3),
解得:![]() <t<
<t<![]() ;
;
即点P在△EFG内部时t的取值范围为:![]() <t<
<t<![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=2(x+3)2+1的顶点坐标是( )
A. (3,1) B. (3,﹣1) C. (﹣3,1) D. (﹣3,﹣1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A. 4a2﹣(2a)2=2a2 B. (﹣a+b)(﹣a﹣b)=a2﹣b2
C. (﹣a2)a3=a6 D. (﹣x)2÷x=﹣x
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个多边形的每一个内角都等于与它相邻的外角的3倍,则这个多边形是几边形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】若点M的坐标为(x,y),且满足xy<0,则点M所在的象限为( )
A. 第一象限或第二象限 B. 第三象限或第四象限 C. 第一象限或第三象限 D. 第二象限或第四象限
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列点中,与点A(2,5)的连线平行于x轴的是( )
A. (2,5) B. (5,2) C. (-2,5) D. (-5,2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)如图所示,下列结论中:
①4ac-b2<0;②3b+2c<0;③4a+c<2b;④m(am+b)+b<a(m≠-1).
其中正确的结论有( )
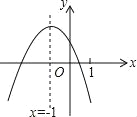
A.1个 B.2个 C.3个 D.4个
相关试题

