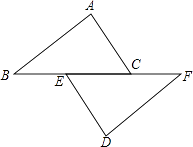
【题目】如图,已知点B,E,C,F在一条直线上,AB=DF,AC=DE,∠A=∠D. 
(1)求证:AC∥DE;
(2)若BF=13,EC=5,求BC的长.
参考答案:
【答案】
(1)证明:在△ABC和△DFE中 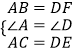 ,
,
∴△ABC≌△DFE(SAS),
∴∠ACE=∠DEF,
∴AC∥DE
(2)解:∵△ABC≌△DFE,
∴BC=EF,
∴CB﹣EC=EF﹣EC,
∴EB=CF,
∵BF=13,EC=5,
∴EB= ![]() =4,
=4,
∴CB=4+5=9.
【解析】(1)首先证明△ABC≌△DFE可得∠ACE=∠DEF,进而可得AC∥DE;(2)根据△ABC≌△DFE可得BC=EF,利用等式的性质可得EB=CF,再由BF=13,EC=5进而可得EB的长,然后可得答案.
-
科目: 来源: 题型:
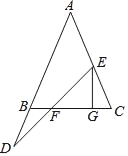
查看答案和解析>>【题目】两个大小不同的等腰直角三角形三角板按图1所示的位置放置,图2是由它抽象出的几何图形,AB=AC,AE=AD,∠BAC=∠EAD=90°,B,C,E在同一条直线上,连接DC.

(1)请找出图2中与△ABE全等的三角形,并给予证明;
(2)证明:DC⊥BE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知2a2+3a﹣6=0,求代数式3a(2a+1)﹣(2a+1)(2a﹣1)的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠ABC=∠C,点E在线段AC上,D在AB的延长线上,且有BD=CE,连接DE交BC于F,过E作FG⊥BC于G.试说明线段EF、FG、CG之间的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E.

(1)若∠A=40°,求∠DBC的度数;
(2)若AE=6,△CBD的周长为20,求△ABC的周长. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:﹣1+3=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:(2a﹣b)(a+2b)﹣(3a+2b)(3a﹣2b),其中a=2,b=﹣3.
相关试题

