【题目】如图,在锐角三角形ABC中,直线l为BC的中垂线,射线m为∠ABC的角平分线,直线l与m相交于点P.若∠BAC=60°,∠ACP=24°,则∠ABP的度数是( )

A. 24° B. 30° C. 32° D. 36°
参考答案:
【答案】C
【解析】
连接PA,根据线段垂直平分线的性质得到PB=PC,得到∠PBC=∠PCB,根据角平分线的定义得到∠PBC=∠ABP,根据三角形内角和定理列式计算即可.
连接PA,如图所示:
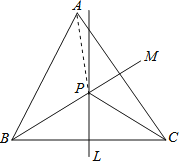
∵直线L为BC的垂直平分线,
∴PB=PC,
∴∠PBC=∠PCB,
∵直线M为∠ABC的角平分线,
∴∠PBC=∠ABP,
设∠PBC=x,则∠PCB=∠ABP=x,
∴x+x+x+60°+24°=180°,
解得,x=32°,
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的对话:
MM:“请帮我称些梨.”
售货员:“您上次买的梨卖没了,您试一试新进的苹果,价格虽然比梨贵些,但苹果营养价
值更高.”
MM:“好,我跟上次一样,也买30元钱.”
对比两次的电脑小票,MM发现:每千克苹果的价格是梨的1.5倍,苹果的重量比梨轻2.5
千克.
根据上面的对话和MM发现,分别求出苹果和梨的单价.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校在践行“社会主义核心价值观”演讲比赛中,对名列前20名的选手的综合分数m进行分组统计,结果如表所示:
组号
分组
频数
一
6≤m<7
2
二
7≤m<8
7
三
8≤m<9
a
四
9≤m≤10
2
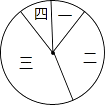
(1)求a的值;
(2)若用扇形图来描述,求分数在8≤m<9内所对应的扇形图的圆心角大小;
(3)将在第一组内的两名选手记为:A1、A2 , 在第四组内的两名选手记为:B1、B2 , 从第一组和第四组中随机选取2名选手进行调研座谈,求第一组至少有1名选手被选中的概率(用树状图或列表法列出所有可能结果). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是( )

A. BC=EC,∠B=∠E B. BC=DC,∠A=∠D
C. BC=EC,AC=DC D. AC=DC,∠A=∠D
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,点O在对角线AC上,以OA的长为半径的圆O与AD、AC分别交于点E、F,且∠ACB=∠DCE.

(1)判断直线CE与⊙O的位置关系,并证明你的结论;
(2)若tan∠ACB=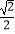 ,BC=2,求⊙O的半径.
,BC=2,求⊙O的半径. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,△ABC为等边三角形,AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S,则四个结论①点P在∠A的平分线上;②AS=AR;③QP∥AR;④△BRP≌△QSP.其中正确的是( )
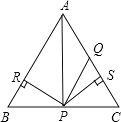
A. ①② B. ①②④ C. ①②③ D. ①②③④
-
科目: 来源: 题型:
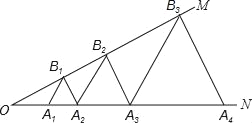
查看答案和解析>>【题目】如图,已知:∠MON=30°,点A1、A2、A3在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A6B6A7的边长为_____.
相关试题

