【题目】如图,某大楼的顶部竖有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底仰角为60°,沿坡度为1: ![]() 的坡面AB向上行走到B处,测得广告牌顶部C的仰角为45°,又知AB=10m,AE=15m,求广告牌CD的高度(精确到0.1m,测角仪的高度忽略不计)
的坡面AB向上行走到B处,测得广告牌顶部C的仰角为45°,又知AB=10m,AE=15m,求广告牌CD的高度(精确到0.1m,测角仪的高度忽略不计)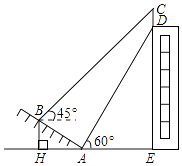
参考答案:
【答案】解:在Rt△ABH中,
∵tan∠BAH= ![]() =
= ![]() =
= ![]() ,
,
∴∠BAH=30°,
∴BH=AB,sin∠BAH=10,sin30°=10× ![]() =5,
=5,
在Rt△ABH中,AH=AB.cos∠BAH=10,cos30°=5 ![]() ,
,
在Rt△ADE中,tan∠DAE= ![]() ,
,
即tan60°= ![]() ,
,
∴DE=15 ![]() ,
,
如图,过点B作BF⊥CE,垂足为F,
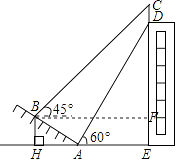
∴BF=AH+AE=5 ![]() +15,
+15,
DF=DE﹣EF=DE﹣BH=15 ![]() ﹣5,
﹣5,
在Rt△BCF中,∠C=90°﹣∠CBF=90°﹣45°=45°,
∴∠C=∠CBF=45°,
∴CF=BF=5 ![]() +15,
+15,
∴CD=CF﹣DF=5 ![]() +15﹣(15
+15﹣(15 ![]() ﹣5)=20﹣10
﹣5)=20﹣10 ![]() ≈20﹣10×1.732≈2.7(米),
≈20﹣10×1.732≈2.7(米),
答:广告牌CD的高度约为2.7米.
【解析】过点B作BF⊥CE,垂足为F,通过解直角三角形求出BH、AH,在△ADE解直角三角形求出DE的长,进而可求出EH即BF的长,在Rt△CBF中,∠CBF=45°,则CF=BF,由此可求出CF的长,最后,根据CD=CF+FE-DE求解即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,AB∶BC∶CA=3∶4∶5,且周长为36 cm,点P从点A开始沿AB边向B点以每秒1cm的速度移动;点Q从点B沿BC边向点C以每秒2cm的速度移动,如果同时出发,则过3s时,△BPQ的面积为____cm2.

-
科目: 来源: 题型:
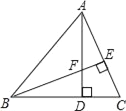
查看答案和解析>>【题目】如图,△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F.
(1)求证:△ADC≌△BDF;
(2)求证:BF=2AE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(π﹣1)0+|2﹣
 |﹣(
|﹣(  )﹣1+
)﹣1+  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点.点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD、AN.

(1)求证:四边形AMDN是平行四边形;
(2)填空:①当AM的值为时,四边形AMDN是矩形; ②当AM的值为时,四边形AMDN是菱形. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上有A、B、C、D四个整数点
 即各点均表示整数
即各点均表示整数 ,且
,且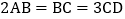 ,若A、D两点表示的数的分别为
,若A、D两点表示的数的分别为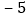 和6,点E为BD的中点,那么该数轴上上述五个点所表示的整数中,离线段BD的中点最近的整数是
和6,点E为BD的中点,那么该数轴上上述五个点所表示的整数中,离线段BD的中点最近的整数是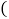
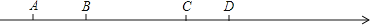
A.
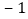 B. 0C. 1D. 2
B. 0C. 1D. 2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,∠C=90°,D为AB的中点,E、F分别在AC、BC上,且DE⊥DF.
求证:AE2+BF2=EF2.

相关试题

