【题目】已知,点A(t,1)是平面直角坐标系中第一象限的点,点B,C分别是y轴负半轴和x轴正半轴上的点,连接AB,AC,BC.
(1)如图1,若OB=1,OC =![]() ,且A,B,C在同一条直线上,求t的值;
,且A,B,C在同一条直线上,求t的值;

(2)如图 2,当 t =1,∠ACO +∠ACB = 180°时,求 BC + OC -OB 的值;

参考答案:
【答案】(1)t=3(2)2.
【解析】
(1)根据OB=1,OC =![]() 得到直线BC的解析式,令y=1,即可求出t的值;
得到直线BC的解析式,令y=1,即可求出t的值;
(2)延长BC至D根据∠ACO +∠ACB = 180°得到AC平分∠OCD,作AG⊥OC,AH⊥BD,根据角平分线的性质得到AG=AH,作AE⊥y轴,由A(1,1)得到AE=AG=AH=1,作AF=AC交y轴于F点,,作AF=AC交y轴于F点,根据HL可证明△AEF≌△AGC,△ABE≌△ABH,则EF=CH,BC=BF,故BC + OC –OB=BF+OG+GC-OB=OB+OF+OG+GC-OB=OF+GC+OG= OF+EF+OG=OE+OG=2.
(1)根据OB=1,OC =![]()
∴B(0,-1),C(![]() ,0),
,0),
设直线BC的解析式为y=kx+b,
代入得
解得
∴直线BC的解析式为y=![]() x-1,令y=1,
x-1,令y=1,
即x=3,
故t=3.
(2)延长BC至D
∵∠ACO +∠ACB = 180°
∴∠ACO=∠ACD,
∴AC平分∠OCD,
作AG⊥OC,AH⊥BD,
∴AG=AH,
作AE⊥y轴,∵A(1,1)得到AE=AG=AH=1,
在y轴上找一点F,使AF=AC,
∵AE=AG,
∠AEF=∠AGC=90°,AF=AC
∴△AEF≌△AGC(HL),
∴EF=CG,
同理可得△ABE≌△ABH,
∴BE=BH,
∴BF=BE-EF,BC=BH-CH
则BC=BF,
故BC+OC–OB=BF+OG+GC-OB=OB+OF+OG+GC-OB=OF+GC+OG= OF+EF+OG=OE+OG
=2.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB丄CD于点E,且AB = CD = AC,若点I是三角形ACE的角平分线的交点,点F是BD的中点.下列结论:①∠AIC= 135°;②BD = BI,③S△AIC = S△BID ;④IF⊥AC.其中正确的是_________(填序号).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A(0,a),B(b,0),C(c,0)是平面直角坐标系中三点,且a,b满足
 .c<3
.c<3
(1)求A,B两点的坐标;
(2)若△ABC的面积为6.
①在图中画出△ABC;
②若△ABP与△ABC全等,直接写出所有符合条件的P点的坐标;
(3)已知∠MAB = ∠ABC,BM = AC,若满足条件的M点有且只有两个,直接写出此时c的取
值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下关于x的各个多项式中,a,b,c,m,n均为常数.
(1)根据计算结果填写下表:
二次项系数
一次项系数
常数项
(2x + l)(x + 2)
2
2
(2x + 1)(3x - 2)
6
-2
(ax + b)( mx + n)
am
bn
(2)已知(x+ 3)2(x + mx +n)既不含二次项,也不含一次项,求m + n的值.
(3) 多项式M与多项式x2-3x + 1的乘积为2x4+ ax3 + bx2+ cx -3,则2 a +b + c的值为
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是
 的直径,弦
的直径,弦 于H,过CD延长线上一点E作
于H,过CD延长线上一点E作 的切线交AB的延长线于
的切线交AB的延长线于 切点为G,连接AG交CD于K.
切点为G,连接AG交CD于K.
 求证:
求证: ;
; 若
若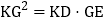 ,试判断AC与EF的位置关系,并说明理由;
,试判断AC与EF的位置关系,并说明理由; 在
在 的条件下,若
的条件下,若 ,
, ,求FG的长.
,求FG的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 过点
过点 ,交x轴于A,B两点
,交x轴于A,B两点 点A在点B的左侧
点A在点B的左侧 .
.
 求抛物线的解析式,并写出顶点M的坐标;
求抛物线的解析式,并写出顶点M的坐标; 连接OC,CM,求
连接OC,CM,求 的值;
的值; 若点P在抛物线的对称轴上,连接BP,CP,BM,当
若点P在抛物线的对称轴上,连接BP,CP,BM,当 时,求点P的坐标.
时,求点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了进一步降低机动车污染物排放,减轻重污染天气污染发生频次和污染程度,保障人民群众身体健康,郑州市从2017年12月4日0时至2017年12月31日24时起对机动车实施单双号限行措施,此次限行将会大大减少空气中
 的排放量,
的排放量, 指的是雾天气时大气中直径小于或等于
指的是雾天气时大气中直径小于或等于 的颗粒物,将
的颗粒物,将 用科学记数法表示为
用科学记数法表示为

A.
 B.
B. 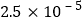 C.
C.  D.
D. 
相关试题

