【题目】如图,抛物线![]() 过点
过点![]() ,交x轴于A,B两点
,交x轴于A,B两点![]() 点A在点B的左侧
点A在点B的左侧![]() .
.

![]() 求抛物线的解析式,并写出顶点M的坐标;
求抛物线的解析式,并写出顶点M的坐标;
![]() 连接OC,CM,求
连接OC,CM,求![]() 的值;
的值;
![]() 若点P在抛物线的对称轴上,连接BP,CP,BM,当
若点P在抛物线的对称轴上,连接BP,CP,BM,当![]() 时,求点P的坐标.
时,求点P的坐标.
参考答案:
【答案】![]() 抛物线的解析式为
抛物线的解析式为![]() ,顶点M的坐标为
,顶点M的坐标为![]() ;
;![]() ;
;![]() P点坐标为
P点坐标为![]() 或
或![]()
【解析】
![]() 根据待定系数法,可得函数解析式;根据顶点式解析式,可得顶点坐标;
根据待定系数法,可得函数解析式;根据顶点式解析式,可得顶点坐标;
![]() 根据勾股定理及逆定理,可得
根据勾股定理及逆定理,可得![]() ,根据正切函数,可得答案;
,根据正切函数,可得答案;
![]() 根据相似三角形的判定与性质,可得PM的值,可得M点坐标.
根据相似三角形的判定与性质,可得PM的值,可得M点坐标.
![]() 由抛物线
由抛物线![]() 过点
过点![]() ,
,
得![]() ,解得
,解得![]() ,
,
![]() 抛物线的解析式为
抛物线的解析式为![]() ,顶点M的坐标为
,顶点M的坐标为![]() ;
;
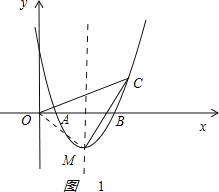
![]() 如图1,连接OM,
如图1,连接OM,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ;
;
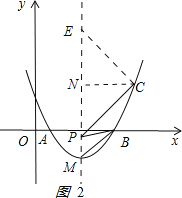
![]() 如图2,过C作
如图2,过C作![]() 对称轴,垂足N在对称轴上,取一点E,使
对称轴,垂足N在对称轴上,取一点E,使![]() ,连接CE,
,连接CE,![]() .
.
当![]() 时,
时,![]() ,解得的
,解得的![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ∽
∽![]() ,
,
![]() ,易知
,易知![]() ,
,![]() ,
,
![]() ,解得
,解得![]() ,
,
P点坐标为![]() 或
或![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下关于x的各个多项式中,a,b,c,m,n均为常数.
(1)根据计算结果填写下表:
二次项系数
一次项系数
常数项
(2x + l)(x + 2)
2
2
(2x + 1)(3x - 2)
6
-2
(ax + b)( mx + n)
am
bn
(2)已知(x+ 3)2(x + mx +n)既不含二次项,也不含一次项,求m + n的值.
(3) 多项式M与多项式x2-3x + 1的乘积为2x4+ ax3 + bx2+ cx -3,则2 a +b + c的值为
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,点A(t,1)是平面直角坐标系中第一象限的点,点B,C分别是y轴负半轴和x轴正半轴上的点,连接AB,AC,BC.
(1)如图1,若OB=1,OC =
 ,且A,B,C在同一条直线上,求t的值;
,且A,B,C在同一条直线上,求t的值;
(2)如图 2,当 t =1,∠ACO +∠ACB = 180°时,求 BC + OC -OB 的值;

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是
 的直径,弦
的直径,弦 于H,过CD延长线上一点E作
于H,过CD延长线上一点E作 的切线交AB的延长线于
的切线交AB的延长线于 切点为G,连接AG交CD于K.
切点为G,连接AG交CD于K.
 求证:
求证: ;
; 若
若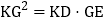 ,试判断AC与EF的位置关系,并说明理由;
,试判断AC与EF的位置关系,并说明理由; 在
在 的条件下,若
的条件下,若 ,
, ,求FG的长.
,求FG的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了进一步降低机动车污染物排放,减轻重污染天气污染发生频次和污染程度,保障人民群众身体健康,郑州市从2017年12月4日0时至2017年12月31日24时起对机动车实施单双号限行措施,此次限行将会大大减少空气中
 的排放量,
的排放量, 指的是雾天气时大气中直径小于或等于
指的是雾天气时大气中直径小于或等于 的颗粒物,将
的颗粒物,将 用科学记数法表示为
用科学记数法表示为

A.
 B.
B. 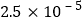 C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】某大型企业为了保护环境,准备购买A、B两种型号的污水处理设备共8台,用于同时治理不同成分的污水,若购买A型2台、B型3台需54万,购买A型4台、B型2台需68万元.
(1)求出A型、B型污水处理设备的单价;
(2)经核实,一台A型设备一个月可处理污水220吨,一台B型设备一个月可处理污水190吨,如果该企业每月的污水处理量不低于1565吨,请你为该企业设计一种最省钱的购买方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列不等式(组)
①

②

把下列各式分解因式:
③
 ;
; ④

化简分式
⑤
 ;
; ⑥(
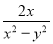 -
- )(x-y)2
)(x-y)2 解方程:
⑦
 ;
; ⑧

相关试题

