【题目】如图,已知A(0,a),B(b,0),C(c,0)是平面直角坐标系中三点,且a,b满足![]() .c<3
.c<3

(1)求A,B两点的坐标;
(2)若△ABC的面积为6.
①在图中画出△ABC;
②若△ABP与△ABC全等,直接写出所有符合条件的P点的坐标;
(3)已知∠MAB = ∠ABC,BM = AC,若满足条件的M点有且只有两个,直接写出此时c的取
值范围.
参考答案:
【答案】(1)A(0,3),B(3,0)(2)①图见解析②(3,4)或(4,3)或(0,-1)(3)3-![]() <c<0
<c<0
【解析】
(1)根据绝对值与平方的非负性即可求出a,b的值,故可求解;
(2)①根据c<3与三角形的面积公式即可得到BC的长,故可求出C点坐标,②根据直角坐标系的特点及全等三角形的性质即可找到P点;
(3)由∠MAB = ∠ABC,BM = AC,结合图形与M点有且只有两个即可得到c的取值.
(1)∵![]()
∴![]()
故a=b=3.
故A(0,3),B(3,0)
(2)①∵C(c,0)
∴C点在x轴上,∵△ABC的面积为6
∴![]() =6
=6
即![]()
解得BC=4,
∵c<3
∴C(-1,0)
②∵△ABP与△ABC全等,如图P点的坐标为(3,4)或(4,3)或(0,-1)

(3)∵∠MAB =∠ABC
所以M在直线y=3上,且在点A的右侧,
∵BM = AC,满足条件的M点有且只有两个,则BM1<BC<AB,
AB=![]() =
=![]()
故3<3-c<![]()
解得3-![]() <c<0
<c<0
故满足条件的M点有且只有两个时,c的取值为3-![]() <c<0.
<c<0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知甲、乙两地相距90km,A,B两人沿同一公路从甲地出发到乙地,A骑摩托车,B骑电动车,图中DE,OC分别表示A,B离开甲地的路程s(km)与时间t(h)的函数关系的图象,根据图象解答下列问题.
(1)A比B后出发几个小时?B的速度是多少?
(2)在B出发后几小时,两人相遇?

-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AD是高,AE是角平分线,已知∠ACB = 70°,∠EAD = 15°,则∠ABC的度数为________
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB丄CD于点E,且AB = CD = AC,若点I是三角形ACE的角平分线的交点,点F是BD的中点.下列结论:①∠AIC= 135°;②BD = BI,③S△AIC = S△BID ;④IF⊥AC.其中正确的是_________(填序号).

-
科目: 来源: 题型:
查看答案和解析>>【题目】以下关于x的各个多项式中,a,b,c,m,n均为常数.
(1)根据计算结果填写下表:
二次项系数
一次项系数
常数项
(2x + l)(x + 2)
2
2
(2x + 1)(3x - 2)
6
-2
(ax + b)( mx + n)
am
bn
(2)已知(x+ 3)2(x + mx +n)既不含二次项,也不含一次项,求m + n的值.
(3) 多项式M与多项式x2-3x + 1的乘积为2x4+ ax3 + bx2+ cx -3,则2 a +b + c的值为
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,点A(t,1)是平面直角坐标系中第一象限的点,点B,C分别是y轴负半轴和x轴正半轴上的点,连接AB,AC,BC.
(1)如图1,若OB=1,OC =
 ,且A,B,C在同一条直线上,求t的值;
,且A,B,C在同一条直线上,求t的值;
(2)如图 2,当 t =1,∠ACO +∠ACB = 180°时,求 BC + OC -OB 的值;

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是
 的直径,弦
的直径,弦 于H,过CD延长线上一点E作
于H,过CD延长线上一点E作 的切线交AB的延长线于
的切线交AB的延长线于 切点为G,连接AG交CD于K.
切点为G,连接AG交CD于K.
 求证:
求证: ;
; 若
若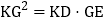 ,试判断AC与EF的位置关系,并说明理由;
,试判断AC与EF的位置关系,并说明理由; 在
在 的条件下,若
的条件下,若 ,
, ,求FG的长.
,求FG的长.
相关试题

