【题目】我们把一个半圆与二次函数图象的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点(半圆与二次函数图象的连接点除外),那么这条直线叫做“蛋圆”的切线.如图,二次函数y=x2﹣2x﹣3的图象与x轴交于点A、B,与y轴交于点D,AB为半圆直径,半圆圆心为点M,半圆与y轴的正半轴交于点C.
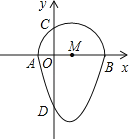
(1)求点C的坐标;
(2)分别求出经过点C和点D的“蛋圆”的切线的表达式.
参考答案:
【答案】(1)(0,![]() );(2)y=
);(2)y=![]() x+
x+![]() ;y=﹣2x﹣3.
;y=﹣2x﹣3.
【解析】
试题分析:(1)连接CM,易求点A,B的坐标,进而可得到AB的长,则圆的半径可求出,再由勾股定理可求出OC的长,继而可求出点C的坐标;
(2)由(1)可知点C的坐标,设过点C的“蛋圆”的切线交x轴于点G,然后根据三角形性质求出G点坐标,用待定系数法求出直线GC的解析式;因为经过点D的“蛋圆”切线过D点,所以本题可设它的解析式为y=kx﹣3.根据图象可求出抛物线的解析式,因为相切,所以它们的交点只有一个,进而可根据一元二次方程的有关知识解决问题.
解:(1)∵二次函数y=x2﹣2x﹣3的图象与x轴交于点A、B,与y轴交于点D,
∴点A(﹣1,0),点B的坐标是(3,0),
∴AB=4,
∵半圆圆心为点M,
∴BM=AM=2,
∴OM=1,
连接CM,
∴OC=![]() =
=![]() ,
,
∴点C的坐标是(0,![]() );
);
(2)设过点C的“蛋圆”的切线交x轴于点G,
∵GC是⊙M的切线,
∴∠GCM=90°,
∴cos∠OMC=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴MG=4,
∴G(﹣3,0),
∴直线GC的表达式为y=![]() x+
x+![]() ;
;
设过点D的直线表达式为y=kx﹣3,
∴![]() ,
,
∴x2﹣(2+k)x=0,
∴△=[﹣(2+k)]2=0,
∴k=﹣2,
∴过点D的“蛋圆”的切线的表达式为y=﹣2x﹣3.
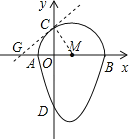
-
科目: 来源: 题型:
查看答案和解析>>【题目】将点A(1,﹣3)沿x轴向左平移3个单位长度,再沿y轴向上平移5个单位长度后得到的点A′的坐标为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中,点P(﹣2,3)关于x轴对称的点的坐标为( )
A.(﹣2,﹣3) B.(2,﹣3) C.(﹣3,﹣2) D.(3,﹣2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠A=90°,∠C=30°,BC=12cm,把△ABC绕着它的斜边中点P逆时针旋转90°至△DEF的位置,DF交BC于点H.△ABC与△DEF重叠部分的面积为( )cm2.

A.8 B.9 C.10 D.12
-
科目: 来源: 题型:
查看答案和解析>>【题目】若等腰三角形的两边长分别4和6,则它的周长是( )
A. 14 B. 15 C. 16 D. 14或16
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O是直线EF上一点,射线OA,OB,OC在直线EF的上方,射线OD的直线EF的下方,且OF平分∠COD,OA⊥OC,OB⊥OD.
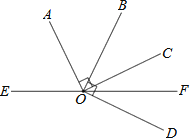
(1)若∠DOF=25°,求∠AOB的度数.
(2)若OA平分∠BOE,则∠DOF的度数是 .(直接写出答案)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在线段、平行四边形、矩形、等腰三角形、圆这几个图形中既是轴对称图形又是中心对称图形的个数是( )
A.2个 B.3个 C.4个 D.5个
相关试题

