【题目】如图,点O是直线EF上一点,射线OA,OB,OC在直线EF的上方,射线OD的直线EF的下方,且OF平分∠COD,OA⊥OC,OB⊥OD.
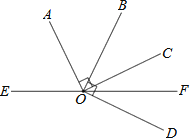
(1)若∠DOF=25°,求∠AOB的度数.
(2)若OA平分∠BOE,则∠DOF的度数是 .(直接写出答案)
参考答案:
【答案】(1)50°;(2)30°.
【解析】
试题分析:(1)利用角平分线的定义可得∠DOC=50°,由垂直的定义可得∠BOD=90°,易得∠BOC=40°,因为OA⊥OC,可得结果;
(2)利用垂直的定义易得∠BOC+∠COD=90°,∠AOB+∠BOC=90°,可得∠COD=∠AOB,设∠DOF=∠COF=x,利用平分线的定义可得∠AOE=∠AOB=∠COD=2x,∠BOC=90°﹣2x,由平角的定义可得5x+90°﹣2x=180°,解得x,即得结果.
解:(1)∵∠DOF=25°,OF平分∠COD,
∴∠DOC=50°,
∵OB⊥OD,
∴∠BOC=90°﹣50°=40°,
∵OA⊥OC,
∴∠AOB=90°﹣∠BOC=50°;
(2)∵∠BOC+∠COD=90°,∠AOB+∠BOC=90°,
∴∠COD=∠AOB,
设∠DOF=∠COF=x,
∵OA平分∠BOE,
∴∠AOE=∠AOB=∠COD=2x,∠BOC=90°﹣2x,
∴5x+90°﹣2x=180°,
解得:x=30°,
即∠DOF=30°.
故答案为:30°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠A=90°,∠C=30°,BC=12cm,把△ABC绕着它的斜边中点P逆时针旋转90°至△DEF的位置,DF交BC于点H.△ABC与△DEF重叠部分的面积为( )cm2.

A.8 B.9 C.10 D.12
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们把一个半圆与二次函数图象的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点(半圆与二次函数图象的连接点除外),那么这条直线叫做“蛋圆”的切线.如图,二次函数y=x2﹣2x﹣3的图象与x轴交于点A、B,与y轴交于点D,AB为半圆直径,半圆圆心为点M,半圆与y轴的正半轴交于点C.
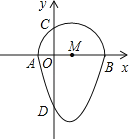
(1)求点C的坐标;
(2)分别求出经过点C和点D的“蛋圆”的切线的表达式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若等腰三角形的两边长分别4和6,则它的周长是( )
A. 14 B. 15 C. 16 D. 14或16
-
科目: 来源: 题型:
查看答案和解析>>【题目】在线段、平行四边形、矩形、等腰三角形、圆这几个图形中既是轴对称图形又是中心对称图形的个数是( )
A.2个 B.3个 C.4个 D.5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据下列条件不能判断△ABC是直角三角形的是( )
A. ∠B=50° ,∠C=40° B. ∠B=∠C=45
C. ∠A,∠B,∠C的度数比为5:3:2 D. ∠A-∠B=90°
-
科目: 来源: 题型:
查看答案和解析>>【题目】将点A(1,﹣3)沿x轴向左平移3个单位长度,再沿y轴向上平移5个单位长度后得到的点A′的坐标为 .
相关试题

