【题目】某活动中心准备带会员去龙潭大峡谷一日游,1张儿童票和2张成人票共需190元,2张儿童票和3张成人票共需300元.
解答下列问题:
(1)求每张儿童票和每张成人票各多少元?
(2)这个活动中心想带50人去游玩,费用不超过3000元,并且出于安全考虑,儿童人数不能超过22人,请你帮助活动中心确立出游方案.
参考答案:
【答案】
(1)解:设每张儿童票x元,每张成人票y元,根据题意,
得 ![]() ,
,
解得: ![]() ,
,
答:每张儿童票30元,每张成人票80元
(2)解:设带儿童m人,根据题意,得30m+80(50﹣m)≤3000,
解得 m≥20,
又∵儿童人数不能超过22人,
∴带儿童人数的取值范围是20≤m≤22;
则方案一:带儿童20人,成人30人;
方案二:带儿童21人,成人29人;
方案三:带儿童22人,成人28人
【解析】(1)设每张儿童票x元,每张成人票y元,根据两家人的购票费用列方程组求解即可;
(2)设带儿童m人,然后依据总费用不超过3000元,并且儿童人数不能超过22人列不等式组求解即可.
【考点精析】关于本题考查的一元一次不等式组的应用,需要了解1、审:分析题意,找出不等关系;2、设:设未知数;3、列:列出不等式组;4、解:解不等式组;5、检验:从不等式组的解集中找出符合题意的答案;6、答:写出问题答案才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正方形ABCD中,BC=3,点E、F分别是CB、CD延长线上的点,DF=BE,连接AE、AF,过点A作AH⊥ED于H点.
(1)求证:△ADF≌△ABE;
(2)若BE=1,求tan∠AED的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】平行四边形ABCD中,对角线AC=12,BD=8,交点为点O,则边AB的取值范围为( )
A.1<AB<2
B.2<AB<10
C.4<AB<10
D.4<AB<20 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,AB=2,∠BAD=60°,过点D作DE⊥AB于点E,DF⊥BC于点F.
(1)如图1,连接AC分别交DE、DF于点M、N,求证:MN=
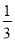 AC;
AC;(2)如图2,将△EDF以点D为旋转中心旋转,其两边DE′、DF′分别与直线AB、BC相交于点G、P,连接GP,当△DGP的面积等于
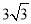 时,求旋转角的大小并指明旋转方向.
时,求旋转角的大小并指明旋转方向.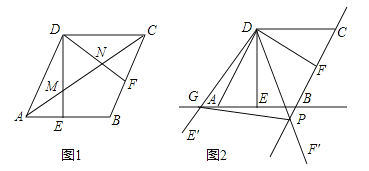
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠A=180°﹣∠ABC,BD⊥CD于D,EF⊥CD于F.

(1)求证:AD∥BC;
(2)若∠1=42°,求∠2的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠MON=30°,点A1 , A2 , A3 , …在射线ON上,点B1 , B2 , B3 , …在射线OM上,△A1B1A2 , △A2B2A3 , △A3B3A4 , …均为等边三角形,若OA1=2,则△A5B5A6的边长为 .
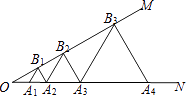
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组
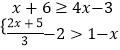 ,并求它的整数解.
,并求它的整数解.
相关试题

