【题目】如图,正方形![]() 的四个顶点都在
的四个顶点都在![]() 上,点
上,点![]() 在
在![]() 上,若
上,若![]() 是
是![]() 上的一点,且
上的一点,且![]() .
.
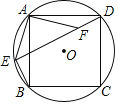
(Ⅰ)求证:![]() ≌
≌![]() ,并指出
,并指出![]() 可以通过怎样的旋转得到
可以通过怎样的旋转得到![]() ;
;
(Ⅱ)求线段![]() 、
、![]() 、
、![]() 之间满足的数量关系.
之间满足的数量关系.
参考答案:
【答案】(Ⅰ)见解析,![]() 以点
以点![]() 为旋转中心、顺时针旋转
为旋转中心、顺时针旋转![]() 得到
得到![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】
(Ⅰ)根据圆周角定理可得:![]() ,再根据正方形的性质得到
,再根据正方形的性质得到![]() ,
,![]() ,利用SAS定理证明
,利用SAS定理证明![]() ≌
≌![]() ,根据旋转的概念解答;
,根据旋转的概念解答;
(Ⅱ)根据全等三角形的性质得到![]() ,
,![]() ,根据等腰直角三角形的性质得到
,根据等腰直角三角形的性质得到![]() ,结合图形计算,得到答案.
,结合图形计算,得到答案.
(Ⅰ)证明:由圆周角定理得,![]() ,
,
∵四边形![]() 是正方形,
是正方形,
∴![]() ,
,![]() .
.
在![]() 和
和![]() 中,
中,
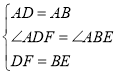 ,
,
∴![]() ≌
≌![]() (SAS),
(SAS),
∵边AD以点![]() 为旋转中心、顺时针旋转
为旋转中心、顺时针旋转![]() 得到边AB
得到边AB
∴![]() 以点
以点![]() 为旋转中心、顺时针旋转
为旋转中心、顺时针旋转![]() 得到
得到![]() .
.
(Ⅱ)解:![]() ,
,
理由如下:∵![]() ≌
≌![]() ,
,
∴![]() ,
,![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() 为等腰直角三角形,
为等腰直角三角形,
∴![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,抛物线
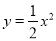 经过点
经过点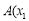 ,
,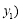 、
、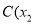 ,
,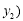 ,其中
,其中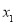 、
、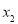 是方程
是方程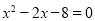 的两根,且
的两根,且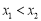 ,过点
,过点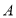 的直线
的直线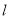 与抛物线只有一个公共点
与抛物线只有一个公共点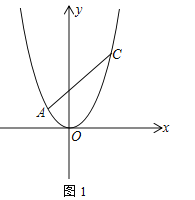
(1)求
 、
、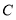 两点的坐标;
两点的坐标;(2)求直线
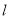 的解析式;
的解析式;(3)如图2,点
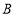 是线段
是线段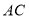 上的动点,若过点
上的动点,若过点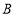 作
作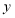 轴的平行线
轴的平行线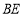 与直线
与直线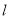 相交于点
相交于点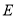 ,与抛物线相交于点
,与抛物线相交于点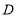 ,过点
,过点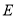 作
作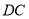 的平行线
的平行线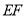 与直线
与直线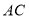 相交于点
相交于点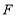 ,求
,求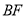 的长.
的长. -
科目: 来源: 题型:
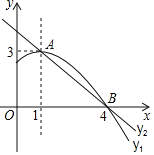
查看答案和解析>>【题目】如图是抛物线
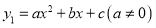 图象的一部分,顶点
图象的一部分,顶点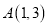 ,与
,与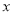 轴的一个交点
轴的一个交点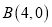 ,直线
,直线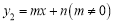 与抛物线交于
与抛物线交于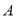 ,
,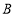 两点,下列结论:
两点,下列结论:①
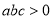 ;
;②
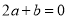 ;
;③当
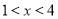 时,有
时,有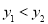 ;
;④方程
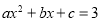 有两个相等的实数根;
有两个相等的实数根;⑤代数式
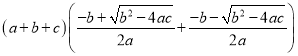 的值是6.
的值是6.其中正确的序号有( )
A.①③④B.②④C.③⑤D.②④⑤
-
科目: 来源: 题型:
查看答案和解析>>【题目】某通讯公司规定:一名客户如果一个月的通话时间不超过
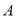 分钟,那么这个月这名客户只要交10元通话费;如果超过
分钟,那么这个月这名客户只要交10元通话费;如果超过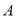 分钟,那么这个月除了仍要交10元通话费外,超过部分还要按每分钟
分钟,那么这个月除了仍要交10元通话费外,超过部分还要按每分钟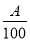 元交费.
元交费.(Ⅰ)某名客户7月份通话90分钟,超过了规定的
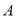 分钟,则超过部分应交通话费______元(用含
分钟,则超过部分应交通话费______元(用含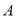 的代数式表示);
的代数式表示);(Ⅱ)下表表示某名客户8月份、9月份的通话情况和交费情况:
月份
通话时间/分钟
通话费总数/元
8月份
80
25
9月份
45
10
根据上表的数据,求
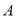 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】定义:若抛物线
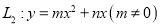 与抛物线
与抛物线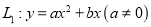 的开口大小相同,方向相反,且抛物线
的开口大小相同,方向相反,且抛物线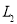 经过
经过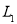 的顶点,我们称抛物线
的顶点,我们称抛物线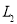 为
为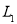 的“友好抛物线”.
的“友好抛物线”.(1)若
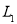 的表达式为
的表达式为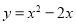 ,求
,求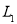 的“友好抛物线”的表达式;
的“友好抛物线”的表达式;(2)已知抛物线
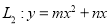 为
为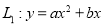 的“友好抛物线”.求证:抛物线
的“友好抛物线”.求证:抛物线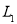 也是
也是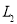 的“友好抛物线”;
的“友好抛物线”;(3)平面上有点
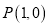 ,
,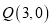 ,抛物线
,抛物线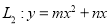 为
为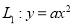 的“友好抛物线”,且抛物线
的“友好抛物线”,且抛物线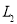 的顶点在第一象限,纵坐标为2,当抛物线
的顶点在第一象限,纵坐标为2,当抛物线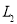 与线段
与线段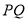 没有公共点时,求
没有公共点时,求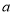 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,E为AD的中点,已知△DEF的面积为S,则四边形ABCE的面积为( )
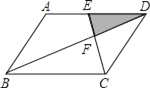
A. 8S B. 9S C. 10S D. 11S
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一条长为20cm的铁丝剪成两段,并以每一段铁丝的长度为周长做成一个正方形.
(1)要使这两个正方形的面积之和等于17cm2,那么这段铁丝剪成两段后的长度分别是多少?
(2)两个正方形的面积之和可能等于12cm2吗? 若能,求出两段铁丝的长度;若不能,请说明理由.
相关试题

