【题目】在平面直角坐标系内,双曲线:y= ![]() (x>0)分别与直线OA:y=x和直线AB:y=﹣x+10,交于C,D两点,并且OC=3BD.
(x>0)分别与直线OA:y=x和直线AB:y=﹣x+10,交于C,D两点,并且OC=3BD. 
(1)求出双曲线的解析式;
(2)连结CD,求四边形OCDB的面积.
参考答案:
【答案】
(1)解:过点A、C、D作x轴的垂线,垂足分别是M、E、F,
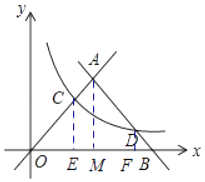
∴∠AMO=∠CEO=∠DFB=90°,
∵直线OA:y=x和直线AB:y=﹣x+10,
∴∠AOB=∠ABO=45°,
∴△CEO∽△DEB
∴ ![]() =
= ![]() =3,
=3,
设D(10﹣m,m),其中m>0,
∴C(3m,3m),
∵点C、D在双曲线上,
∴9m2=m(10﹣m),
解得:m=1或m=0(舍去)
∴C(3,3),
∴k=9,
∴双曲线y= ![]() (x>0)
(x>0)
(2)解:由(1)可知D(9,1),C(3,3),B(10,0),
∴OE=3,EF=6,DF=1,BF=1,
∴S四边形OCDB=S△OCE+S梯形CDFE+S△DFB
= ![]() ×3×3+
×3×3+ ![]() ×(1+3)×6+
×(1+3)×6+ ![]() ×1×1=17,
×1×1=17,
∴四边形OCDB的面积是17
【解析】(1)过点A、C、D作x轴的垂线,垂足分别是M、E、F,由直线y=x和y=﹣x+10可知∠AOB=∠ABO=45°,证明△CEO∽△DEB,从而可知 ![]() =
= ![]() =3,然后设设D(10﹣m,m),其中m>0,从而可知C的坐标为(3m,3m),利用C、D在反比例函数图象上列出方程即可求出m的值.(2)求分别求出△OCE、△DFB△、梯形CDFE的面积即可求出答案.
=3,然后设设D(10﹣m,m),其中m>0,从而可知C的坐标为(3m,3m),利用C、D在反比例函数图象上列出方程即可求出m的值.(2)求分别求出△OCE、△DFB△、梯形CDFE的面积即可求出答案.
-
科目: 来源: 题型:
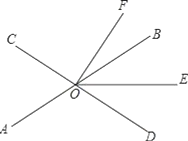
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,OE平分∠BOD.
(1)若∠AOC=70°,∠DOF=90°,求∠EOF的度数;
(2)若OF平分∠COE,∠BOF=15°,若设∠AOE=x°.
①用含x的代数式表示∠EOF;
②求∠AOC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知P点是∠AOB平分线上一点,PC⊥OA,PD⊥OB,垂足为C、D.
(1)求证:∠PCD=∠PDC;
(2)求证:OP是线段CD的垂直平分线.

-
科目: 来源: 题型:
查看答案和解析>>【题目】数学兴趣小组想利用所学的知识了解某广告牌的高度(图中GH的长),经测量知CD=2m,在B处测得点D的仰角为60°,在A处测得点C的仰角为30°,AB=10m,且A、B、H三点共线,请根据以上数据计算GH的长(
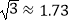 ,要求结果精确得到0.1m)
,要求结果精确得到0.1m)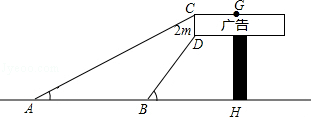
-
科目: 来源: 题型:
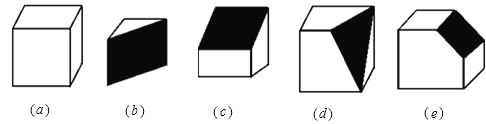
查看答案和解析>>【题目】(10分)下列图形中,图(a)是正方体木块,把它切去一块,得到如图(b)(c)(d)(e)的木块.

(1)我们知道,图(a)的正方体木块有8个顶点、12条棱、6个面,请你将图(b)、(c)、(d)、(e)中木块的顶点数、棱数、面数填入下表;
(2)上表,各种木块的顶点数、棱数、面数之间的数量关系可以归纳出一定的规律,请你试写出顶点数x、棱数y、面数z之间的数量关系式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列不等式,并把它们的解集分别表示在数轴上.
(1)
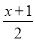 ≥3(x-1)-4;
≥3(x-1)-4;(2)
 -
- ≥1.
≥1. -
科目: 来源: 题型:
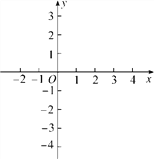
查看答案和解析>>【题目】在下列平面直角坐标系中画出函数y1=-x+3,y2=3x-4的图象.观察图象,回答下列问题:
(1)当x取何值时,y1=y2?
(2)当x取何值时,y1>y2?
(3)当x取何值时,y1<y2?
相关试题

